CORDE DI UNA CIRCONFERENZA
- La circonferenza e il cerchio
- Parti di una circonferenza e di un cerchio
- Il segmento
- Figure geometriche equivalenti e figure geometriche congruenti
- Triangolo isoscele
- Altezze di un triangolo
- Mediane
- Elementi e punti notevoli del triangolo isoscele
- Rette perpendicolari
Chiamiamo CORDA un SEGMENTO che UNISCE DUE PUNTI QUALSIASI di una CIRCONFERENZA.
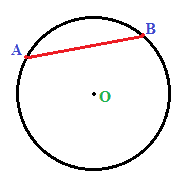
Nell'immagine sopra abbiamo scelto due punti qualsiasi della circonferenza: il punto A e il punto B.
Quindi abbiamo tracciato il segmento che unisce questi due punti: il segmento AB è una CORDA della CIRCONFERENZA.
Ora disegniamo la corda MN tale che essa passi per il centro O:
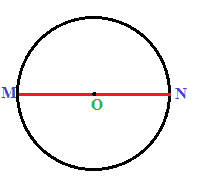
La corda che abbiamo disegnato prende il nome di DIAMETRO della CIRCONFERENZA.
Quindi diciamo che il DIAMETRO è la CORDA che PASSA per il CENTRO.
Essa viene indicata con una d minuscola. E' abbastanza evidente che il DIAMETRO è il DOPPIO del RAGGIO.
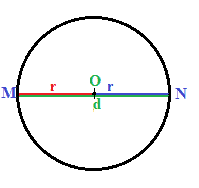
Quindi
d = 2r.
Ovviamente tutti i diametri di una stessa circonferenza sono tra loro congruenti.
Ora consideriamo una circonferenza con centro O e raggio r e disegniamo la corda AB:
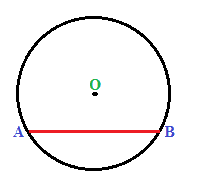
Ora tracciamo il raggio OA e OB:
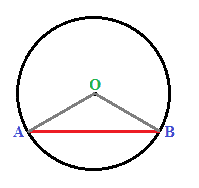
Il triangolo AOB è senz'altro un TRIANGOLO ISOSCELE dato che OA e OB sono i raggi della circonferenza e sono tra loro CONGRUENTI.
Disegniamo ora l'ALTEZZA DEL TRIANGOLO OH:
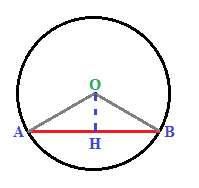
In un TRIANGOLO ISOSCELE, l'ALTEZZA e la MEDIANA COINCIDONO.
Ricordiamo che la MEDIANA è il SEGMENTO che UNISCE un VERTICE al PUNTO MEDIO DEL LATO OPPOSTO.
Quindi il punto H è il PUNTO MEDIO del segmento AB. Di conseguenza AH e HB hanno la stessa lunghezza.
Possiamo dire, allora, che la PERPENDICOLARE condotta dal centro di una circonferenza ad una CORDA la DIVIDE A META'.
E viceversa si può affermare che la PERPENDICOLARE ad una corda AB, nel suo PUNTO MEDIO, PASSA per il CENTRO della circonferenza a cui appartiene la corda.
Notiamo, inoltre, che il segmento OH è la DISTANZA DELLA CORDA dal CENTRO.
Ora, data la nostra circonferenza, disegniamo due CORDE CONGRUENTI AB e CD:
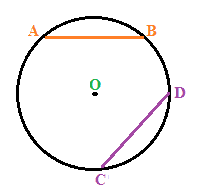
Uniamo i loro estremi con il centro in modo da avere i triangoli AOB e COD:
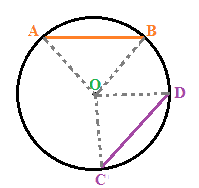
Ora
- OA;
- OB;
- OC;
- OD;
sono CONGRUENTI essendo tutti raggi della circonferenza.
Le BASI dei due TRIANGOLI sono CONGRUENTI dato che all'inizio abbiamo disegnato due corde congruenti.
Di conseguenza, i due TRIANGOLI AOB e COD sono CONGRUENTI.
Se i due triangoli sono congruenti, anche le loro ALTEZZE OH e OK sono CONGRUENTI:
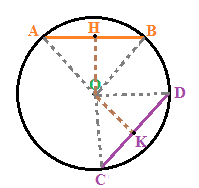
Ma le due altezze sono anche le DISTANZE delle due CORDE dal centro.
Quindi possiamo dire che se due CORDE di una stessa circonferenza sono CONGRUENTI esse hanno UGUALE DISTANZA dal CENTRO.






