DISTANZA TRA DUE PUNTI AVENTI LA STESSA ORDINATA
- Assi cartesiani ortogonali
- Rappresentazione di un punto su un pianto cartesiano
- Rappresentazione di un punto su un pianto cartesiano: alcuni esempi
- Il punto
- Il segmento
- I numeri relativi
DISEGNIAMO SUL PIANO CARTESIANO i punti A e B tali che
A (2; 4)
B (7; 4).
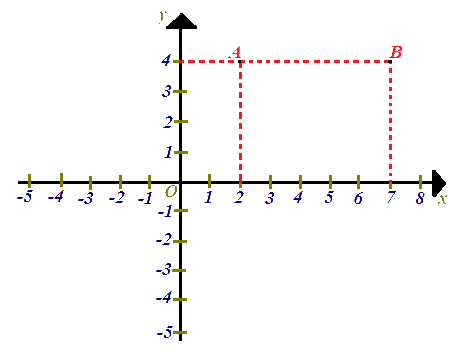
Come possiamo notare i due punti A e B hanno la STESSA ORDINATA.
Ora ci poniamo l'obiettivo di determinare la DISTANZA TRA I DUE PUNTI disegnati.
E' evidente che tale distanza è rappresentata dal SEGMENTO AB:
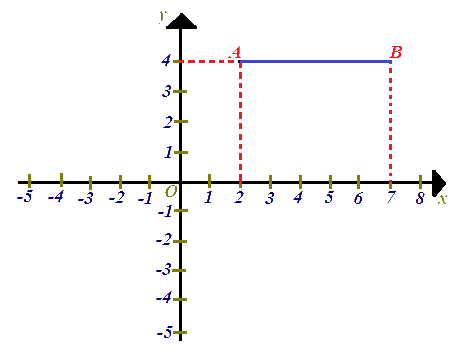
Osserviamo ora la lunghezza di questo
segmento: essa è pari a 5,
infatti l'unità
di misura da noi scelta 
è
contenuta 5 volte nel segmento AB:
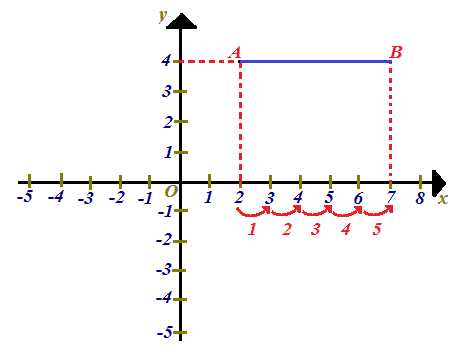
Osserviamo però, che 5 è anche la DIFFERENZA tra l'ASCISSA di B e l'ASCISSA di A. Infatti:
7 - 2 = 5.
Vediamo un altro esempio.
Vogliamo calcolare la DISTANZA TRA I PUNTI
C (-3; 3)
D (4; 3).
Anche in questo caso i due punti hanno la STESSA ORDINATA.
La distanza tra essi è data dal SEGMENTO CD:
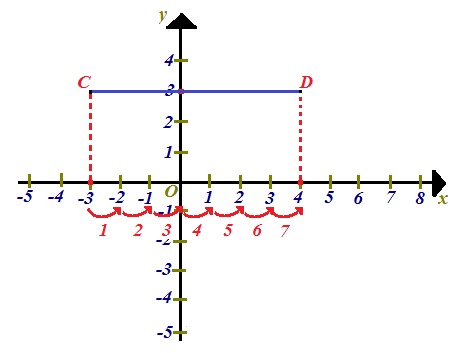
Osserviamo che la lunghezza di questo
segmento è pari a 7,
infatti l'unità
di misura da noi scelta
è
contenuta 7 volte nel segmento CD.
Notiamo, però, che 7 è anche la DIFFERENZA tra l'ASCISSA di D e l'ASCISSA di C. Infatti:
4 - (-3) = 4 + 3 = 7.
Possiamo quindi affermare che per calcolare la differenza tra due punti, aventi la stessa ordinata, è sufficiente calcolare la differenza tra le loro ascisse.
Bisogna, però, fare attenzione a sottrarre dall'ascissa maggiore quella minore e non il contrario. Infatti, se nell'esempio precedente noi avessimo fatto:
-3 - 4 = -7
avremmo ottenuto un valore negativo, ma la MISURA DI UN SEGMENTO è sempre un NUMERO POSITIVO.
Può anche capitare di non conoscere quale dei due punti abbia un'ascissa maggiore. Per evitare questi inconvenienti si prende come distanza dei due punti, il VALORE ASSOLUTO della differenza tra le loro ascisse: in questo caso possiamo prendere le ascisse con qualsiasi ordine.
Quindi possiamo affermare che dati DUE PUNTI aventi la STESSA ORDINATA
A (x1 ; y)
che si legge
punto A di coordinate x con 1 ed y;
e
B (x2 ; y)
che si legge
punto B di coordinate x con 2 ed y;
la DISTANZA TRA I DUE PUNTI è data dal VALORE ASSOLUTO della DIFFERENZA tra le loro ASCISSE, prese con qualsiasi ordine.
In altre parole possiamo scrivere:
AB = |x2 - x1|.
Nella prossima lezione vedremo come calcolare la distanza tra due punti aventi la stessa ascissa.
