DISTANZA TRA DUE PUNTI SUL PIANO CARTESIANO
- Distanza tra due punti aventi la stessa ordinata
- Distanza tra due punti aventi la stessa ascissa
- Distanza tra due punti sul piano
- Il punto
- Radice quadrata di una potenza
- I numeri relativi
Dopo aver visto nelle lezioni precedenti come calcolare la DISTANZA TRA DUE PUNTI sul piano cartesiano, vogliamo ora fare alcune osservazioni.
Partiamo dalla formula che ci permette di trovare la distanza tra due punti che non hanno la stessa ascissa, né la stessa ordinata.
Abbiamo detto che, dati due punti
A (x1 ; y1)
e
B (x2 ; y2)
la distanza tra essi si calcola nel modo seguente:
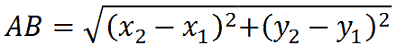 .
.
Ora osserviamo che da questa formula possiamo ottenere anche quelle della distanza di due punti aventi la stessa ordinata e della distanza di due punti aventi la stessa ascissa.
Supponiamo che i punti A e B abbiamo la STESSA ORDINATA, ovvero che
y1 = y2.
Di conseguenza
y2 - y1 = 0.
Quindi, nella formula precedente, avremo:
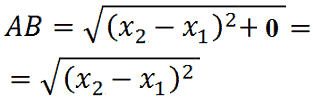
Noi sappiamo che la radice quadrata di un quadrato è uguale al numero stesso, quindi possiamo scrivere:

Non dimentichiamo, nella formula precedente, di indicare il VALORE ASSOLUTO perché, come abbiamo già avuto modo di dire, la misura di un segmento è sempre un numero positivo.
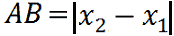
Siamo giunti così allo stesso risultato che avevamo visto in precedenza, cioè che la DISTANZA TRA DUE PUNTI AVENTI LA STESSA ORDINATA è data dal VALORE ASSOLUTO della DIFFERENZA tra le loro ASCISSE.
Supponiamo, ora, che i punti A e B abbiamo la STESSA ASCISSA, ovvero che
x1 = x2.
Di conseguenza
x2 - x1 = 0.
Quindi, nella formula precedente, avremo:
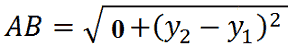
Ovvero:
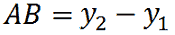
Anche in questo caso andiamo ad indicare il VALORE ASSOLUTO sempre perché la misura di un segmento è un numero positivo.
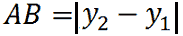
Ancora una volta siamo giunti così allo stesso risultato che avevamo visto in precedenza, cioè che la DISTANZA TRA DUE PUNTI AVENTI LA STESSA ASCISSA è data dal VALORE ASSOLUTO della DIFFERENZA tra le loro ORDINATE.






