FORMULA DI ADDIZIONE DELLA TANGENTE
- Formule goniometriche
- Seconda relazione fondamentale della goniometria
- Formula di addizione del coseno
- Formula di addizione del seno
- Grafico della funzione coseno
Esaminiamo, ora, la FORMULA di ADDIZIONE della TANGENTE, cioè quella formula che ci permette di trovare la TANGENTE della SOMMA degli angoli α e β.
Iniziamo con lo scrivere:
tan (α + β)
Noi sappiamo, dalla SECONDA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA, che la tangente di un angolo non è altro che il rapporto tra il seno e il coseno dell'angolo stesso, ovvero:

Quindi, sostituendo la seconda alla prima, possiamo scrivere:
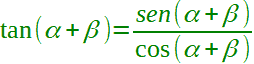
Chiaramente, affinché la frazione abbia significato è necessario che il suo denominatore sia diverso da zero. Pertanto, dobbiamo porre la condizione che
cos (α + β) ≠ 0
Se andiamo a guardare il grafico della funzione coseno vediamo che il coseno di un angolo è uguale a 0 quando l'angolo è pari a π/2 e a (3/2 π). Questo significa che il coseno di un angolo è uguale a zero ogni π radianti a partire da π/2.
Di conseguenza, la condizione che dobbiamo porre è:
α + β ≠ (π/2) + kπ con k ∈ Z
Tornando alla nostra formula
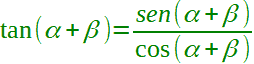
possiamo notare che, a numeratore abbiamo il seno della somma di due angoli, mentre a denominatore abbiamo il conseno della somma di due angoli. Sapendo che:
sen (α + β) = sen α · cos β + cos α · sen β
e che
cos (α + β) = cos α · cos β - sen α · sen β
possiamo scrivere:
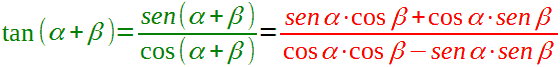
Ora dividiamo, numeratore e denominatore, per il prodotto tra cos α e cos β:
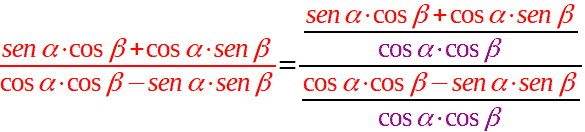
Per poter eseguire questa divisione dobbiamo porre come condizione che
cos α · cos β ≠ 0
cosa che si verifica quando:
cos α ≠ 0
e
cos β ≠ 0
Come abbiamo detto prima, il coseno di un angolo è pari a zero quando l'angolo è pari a (π/2) +kπ.
Quindi, le condizioni da porre sono:
α ≠ (π/2) + kπ
e
β ≠ (π/2) + kπ
con con k ∈ Z
Poste le opportune condizioni, possiamo scrivere la nostra formula nella forma seguente:

A questo punto andiamo a semplificare:

Ricordando che la tangente di un angolo è data dal rapporto tra il seno e il coseno dell'angolo stesso, la nostra formula diventa:

Quindi possiamo dire che la TANGENTE della SOMMA di due ANGOLI è uguale al RAPPORTO che vede al numeratore la SOMMA delle TANGENTI dei due angoli e al denominatore la DIFFERENZA tra 1 e il PRODOTTO delle tangenti dei due angoli. Ovvero:
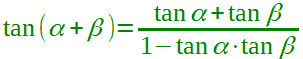
con
α + β ≠ (π/2) + kπ
α ≠ (π/2) + kπ
β ≠ (π/2) + kπ
con
con k ∈ Z
Nella prossima lezione andremo a vedere la formula di sottrazione della tangente.






