ROMBO
- Classificazione dei quadrilateri
- Parallelogramma
- Proprietà del parallelogramma
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Triangolo rettangolo
- Angolo retto - angolo acuto - angolo ottuso
- Rette perpendicolari
Disegniamo un PARALLELOGRAMMA avente tutti e quattro i LATI CONGRUENTI:
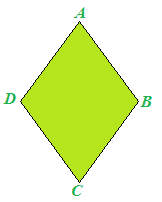
La figura che abbiamo disegnato prende il nome di ROMBO. Quindi il ROMBO è un PARALLELOGRAMMA avente tutti e quattro i LATI CONGRUENTI:
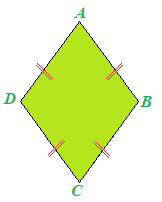
Poiché i lati del rombo hanno tutti la stessa lunghezza esso è un POLIGONO EQUILATERO.
Nel ROMBO, normalmente, non si distinguono la base e l'altezza, ma si parla genericamente di LATI.
Se, tuttavia, vogliamo prendere un lato come BASE, ad esempio il lato BC:
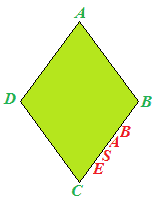
l'ALTEZZA è rappresentata dalla PERPENDICOLARE che UNISCE la BASE ad un VERTICE DEL LATO OPPOSTO:
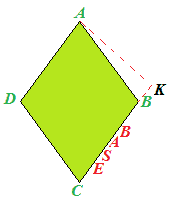
Il segmento AK rappresenta l'altezza nel caso in cui assumiamo il lato BC come base.
Ora disegniamo una delle DIAGONALI del rombo:
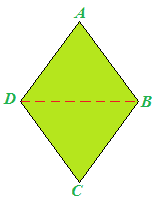
La diagonale divide il rombo in due triangoli ABD e BCD:
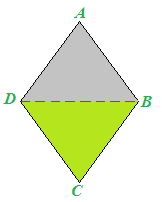
Se proviamo a ritagliare i due triangoli e a sovrapporli l'uno all'altro, noteremo che essi sono congruenti:
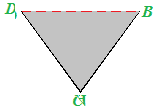
Ciò significa che la diagonale DB
divide esattamente in due parti uguali gli angoli  e
e  .
Di conseguenza possiamo dire che la diagonale DB
è la BISETTRICE
degli angoli
.
Di conseguenza possiamo dire che la diagonale DB
è la BISETTRICE
degli angoli  e
e  .
.
Disegniamo, ora, la diagonale AC:
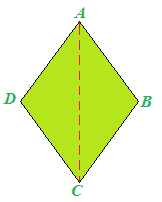
La diagonale divide il rombo in due triangoli ADC e ABC:
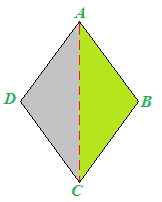
Se proviamo a ritagliare i due triangoli e a sovrapporli l'uno all'altro, noteremo che essi sono congruenti:

Ciò significa che la diagonale AC
divide esattamente in due parti uguali gli angoli 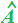 e
e 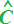 .
Di conseguenza possiamo dire che la diagonale AC
è la BISETTRICE
degli angoli
.
Di conseguenza possiamo dire che la diagonale AC
è la BISETTRICE
degli angoli 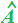 e
e 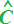 .
.
Da quanto abbiamo affermato segue che i triangoli AOB, BOC, COD, DOA sono congruenti. Essi sono tutti TRIANGOLI RETTANGOLI.
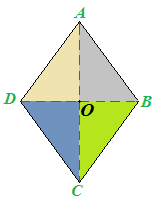
Gli angoli 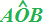 ,
,
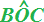 ,
,
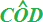 e
e 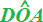 sono tutti ANGOLI
RETTI. Questo significa che le due DIAGONALI
sono PERPENDICOLARI
tra loro.
sono tutti ANGOLI
RETTI. Questo significa che le due DIAGONALI
sono PERPENDICOLARI
tra loro.
Essendo il ROMBO un PARALLELOGRAMMA esso gode di tutte le PROPRIETA' dei parallelogrammi. Ovvero:
- ogni DIAGONALE divide il rombo in DUE TRIANGOLI CONGRUENTI;
- le DIAGONALI si TAGLIANO a META'. Inoltre, nel rombo, le diagonali sono PERPENDICOLARI e sono BISETTRICI degli angoli;
- come in tutti i parallelogrammi i lati opposti sono congruenti, ma nel rombo possiamo affermare che tutti i LATI sono CONGRUENTI (quindi non solo i lati opposti);
- gli ANGOLI OPPOSTI sono CONGRUENTI.






