GRAFICO DELLA FUNZIONE COTANGENTE
Nelle lezioni precedenti abbiamo visto cosa si intende per COTANGENTE e come variano i valori della contangente al variare dell'angolo α.
In questa lezione, invece, andremo a vedere come si presenta il GRAFICO della FUNZIONE COTANGENTE.

Per ottenere il grafico occorre riportare:
- sull'asse delle ASCISSE i valori degli ANGOLI;
- sull'asse delle ORDINATE il corrispondente valore della COTANGENTE. Questo valore può essere determinato calcolando la tangente dell'angolo e successivamente il suo reciproco.
Vediamo quali caratteristiche presenta la nostra funzione.
Iniziamo col dire che il grafico della cotangente prende il nome di COTANGENTOIDE.
All'origine degli assi la funzione cotangente NON è DEFINITA, mentre quando l'angolo α ha un'ampiezza di π/2 la funzione assume valore 0. Ma vediamo cosa accade intorno al punto π:
- per valori inferiori a π, mano a mano che l'angolo si avvicina sempre più a questo valore, la cotangente tende a diventare sempre più piccola.
Per questo diciamo che essa tende a
-∞ (che si legge meno infinito);

- per valori superiori a π mano a mano che l'angolo si avvicina sempre più a questo valore la cotangente tende a diventare sempre più grande.
Per questo diciamo che essa tende a
+∞ (che si legge più infinito).
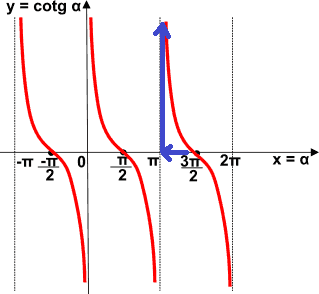
Quando il valore dell'angolo α si avvicina a π la cotangente si avvicina sempre più alla retta parallela all'asse delle y di equazione
x = π
che prende il nome di ASINTOTO VERTICALE del grafico.
Gli asintoti verticali si hanno in corrispondenza degli angoli che misurano -π, 0, π, 2π, ecc...

Quindi possiamo dire che gli asintoti verticali sono le rette di equazione
x = 0 + kπ
con k appartenente all'insieme Z, cioè all' insieme dei numeri interi relativi.
Come si può notare la funzione tangente NON è LIMITATA dato che può assumere qualsiasi valore reale.
Il CODOMINIO della cotangente è dato dall'insieme R dei numeri reali.
La funzione COTANGENTE è una funzione PERIODICA: il periodo è π.

Nel grafico sottostante mettiamo a confronto la funzione tangente con la funzione cotangente.







