ARCHI OPPOSTI
- Archi associati. Riduzione al primo quadrante
- Punti simmetrici rispetto ad una retta
- Seno e coseno
- Tangente
- Cotangente
- Secante
- Cosecante
Disegniamo la circonferenza goniometrica e l'angolo orientato α:

Abbiamo chiamato P il punto associato all'angolo orientato α. Tale punto ha come coordinate il coseno e il seno dell'angolo α. Quindi possiamo scrivere:
P (cos α ; sen α).
Ora andiamo a disegnare il punto P1 (che si legge P con uno) SIMMETRICO di P rispetto all'asse delle x.

Essendo il punto P1 simmetrico a P rispetto all'asse delle ascisse esso avrà come coordinate:
P1 (cos α ; -sen α)
Notiamo ora che il punto P1 è il punto associato all'angolo orientato β:

Ora vogliamo capire quanto vale l'angolo β o meglio, vogliamo capire come possiamo esprimere l'angolo β in termini di α: il che significa RIDURRE l'angolo β al PRIMO QUADRANTE.
Costruiamo il triangolo OHP1 e confrontiamolo con il triangolo OHP:

Osserviamo che, entrambi i triangoli hanno un angolo retto: quello con vertice in H in quanto la retta PP1 è perpendicolare all'asse delle x. Quindi entrambi sono TRIANGOLI RETTANGOLI.

Nei due triangoli sono CONGRUENTI:
- l'ipotenusa, infatti, sia OP che OP1 sono RAGGI della circonferenza goniometrica e quindi, sono pari ad 1
- il cateto OH che è comune ad entrambi i triangoli.

Ma noi sappiamo che due triangoli rettangoli che hanno l'ipotenusa ed un cateto congruenti, sono congruenti. Di conseguenza l'ampiezza dell'angolo α e dell'angolo β sarà la stessa, ma trattandosi di angoli orientati possiamo scrivere che:
β = -α

Di conseguenza, essendo:
P1 (cos α ; -sen α)
possiamo dire che:
sen (-α) = -sen α
cos (-α) = cos α
Dalle due funzioni goniometriche fondamentali possiamo ricavare tutte le altre.
Quindi:

Poiché abbiamo appena visto che
sen (-α) = -sen α
e che
cos (-α) = cos α
possiamo scrivere:

e ricordando che
tan α = sen α/cos α
possiamo scrivere:
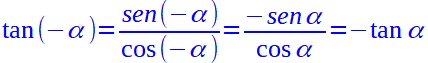
Procediamo in maniera analoga per trovare le altre funzioni goniometriche:



Così, ad esempio, se abbiamo un angolo di -30° e vogliamo conoscere il suo seno, basterà sapere che il seno dell'angolo opposto, cioè dell'angolo di 30°, è pari ad 1/2: di conseguenza il seno dell'angolo di -30° è pari a -1/2.






