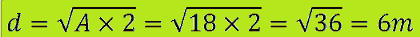AREA DEL QUADRATO CONOSCENDO LA DIAGONALE
- Poligoni equivalenti
- Area dei poligoni
- Area del rombo
- Area del rombo e formule inverse
- Area del quadrato
- Area del quadrato e formule inverse
- Misure di superficie
- Parallelogramma
- Rombo
- Quadrato
Abbiamo visto che l'AREA del QUADRATO si ottiene MOLTIPLICANDO la misura del LATO per SE STESSA. Ovvero:
A = l x l = l2
dove
A é l'area del quadrato
l è il lato.
Vediamo, ora, come è possibile calcolare l'AREA del QUADRATO conoscendo solamente la misura della DIAGONALE.
Dallo studio del QUADRATO sappiamo che esso è un PARALLELOGRAMMA avente tutti e quattro i LATI CONGRUENTI e tutti e quattro gli ANGOLI CONGRUENTI.
Come sappiamo anche il ROMBO ha tutti i lati congruenti.
Inoltre nel QUADRATO le DIAGONALI sono CONGRUENTI, cosa che non accade, normalmente, nel rombo.
Quindi possiamo affermare che il QUADRATO è un ROMBO PARTICOLARE con le diagonali congruenti.
Di conseguenza, per trovare l'AREA del QUADRATO, se conosciamo la misura della sua diagonale, possiamo applicare la formula per il calcolo dell'area del rombo, ovvero:
A = (d1 x d2)/2
dove
A é l'area del quadrato
d1 è una delle diagonali
d2 è l'altra diagonale.
Ma, poiché nel quadrato, le due diagonali sono congruenti, possiamo scrivere la formula precedente in questo modo:
A = (d x d)/2 = d2/2>.
La formula inversa è:
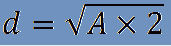
Esempio 1:
calcolare l'area di un quadrato la cui diagonale misura cm 7.
Applichiamo la formula:
A = d2/2 = 72/2 = cm2 24,5.
L'area del rombo è di cm2 24,5.
Esempio 2:
l'area di un quadrato misura m2 18. Quanto misura la sua diagonale?
Applichiamo la formula inversa