AREA DEL TRAPEZIO
- Poligoni equivalenti
- Area dei poligoni
- Area del parallelogramma
- Misure di superficie
- Trapezio
- Parallelogramma
- Rette parallele
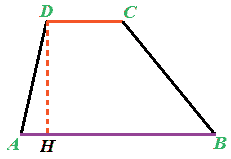
Disegniamo un TRAPEZIO ABCD:
Ora disegniamo un trapezio ad esso congruente che chiamiamo A'B'C'D':
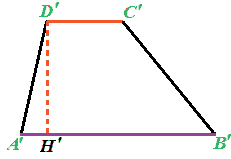
Ritagliamo i due trapezi e li posizioniamo uno accanto all'altro nel modo seguente:

Abbiamo ottenuto un PARALLELOGRAMMA.
Ora osserviamo attentamente il parallelogramma e confrontiamolo con il trapezio di partenza:
Il TRAPEZIO ha altezza DH.
Il PARALLELOGRAMMA ha altezza DH.
La base minore del TRAPEZIO è DC, la base maggiore è AB.
La base del PARALLELOGRAMMA è uguale a AB + D'C'.
Ma D'C' è congruo con DC.
Quindi la base del parallelogramma è
AB + DC.


Il nostro PARALLELOGRAMMA quindi ha:
- per altezza la STESSA ALTEZZA del trapezio;
- per base la SOMMA delle BASI del trapezio.
L'AREA DEL TRAPEZIO è esattamente la META' dell'area del parallelogramma.
In altre parole un TRAPEZIO è EQUIVALENTE alla META' di un PARALLELOGRAMMA che ha per altezza la STESSA ALTEZZA del trapezio e per base la SOMMA DELLE BASI del trapezio.
Quindi, l'AREA del TRAPEZIO si ottiene MOLTIPLICANDO la SOMMA delle misure delle BASI per la misura dell'ALTEZZA e DIVIDENDO il prodotto ottenuto per 2.
La formula sarà:

dove
A é l'area del trapezio
h è l'altezza
b1 è la base maggiore
b2 è la base minore.
Esempio:
calcolare l'area di un trapezio le cui basi misurano rispettivamente m 5 e m 7 e la cui altezza misura m 3.
Applichiamo la formula:
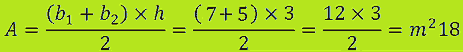
L'area del trapezio è di m2 18.
Nella prossima lezione vedremo le formule inverse.






