CORRISPONDENZA UNIVOCA
Consideriamo l'insieme A costituito da alcuni ragazzi che indicheremo con le lettere:
a, b, c, d, e, f, g.
Consideriamo ora l'insieme B formato da 5 uomini che indicheremo con le lettere:
s, t, u, v, z.
Rappresentiamo i due insiemi con il Diagramma di Venn.
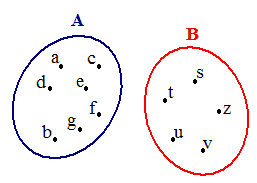
Supponiamo ora che:
- a, b siano figli di s;
- c, d, e siano figli di t;
- f sia figlio di u;
- g sia figlio di v.
In questo modo ad ogni ragazzo dell'insieme A corrisponde un solo elemento dell'insieme B, ma non il contrario. Nel senso che un padre, cioè un elemento dell'insieme B, può avere più figli. Inoltre vi è un uomo, indicato dall'elemento z dell'insieme B, che non è padre di nessun ragazzo dell'insieme A.
In questo modo abbiamo stabilito una RELAZIONE di A in B o anche una RELAZIONE tra A e B.
Nel nostro esempio la relazione tra i due insiemi è rappresentata dall'essere figlio di.
Generalizzando possiamo dire che una RELAZIONE tra due insiemi A e B è un insieme di coppie ordinate formate ognuna da un elemento di A e da un elemento di B.
Le nostre coppie ordinate saranno
(a, s), (b, s), (c, t), (d, t), (e, t), (f, u), (g, v).
Tale relazione prende il nome di CORRISPONDENZA.
Graficamente, per indicare che A è il figlio di s disegniamo una FRECCIA che collega l'elemento a dell'insieme A all'elemento s dell'insieme B.
Chiaramente disegneremo un freccia per collegare, ogni ragazzo dell'insieme A, con il rispettivo padre indicato nell'insieme B. Quindi avremo:
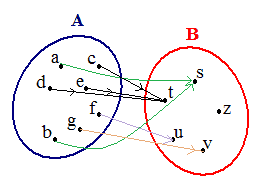
L'insieme delle frecce da noi disegnate rappresenta le coppie che soddisfano la relazione essere figlio di.
La CORRISPONDENZA che abbiamo illustrato prende il nome di CORRISPONDENZA UNIVOCA.
Una CORRISPONDENZA tra due insiemi A e B si dice UNIVOCA se essa ASSOCIA ad OGNI ELEMENTO di A un SOLO ELEMENTO di B, ma non viceversa.
- Coppie ordinate
- Relazione di un insieme A in un insieme B
- Relazione tra insiemi
- Rappresentazione grafica di una relazione
- Relazione tra insiemi
- Grafico di una relazione
- Relazioni inverse
- Rappresentazione grafica di una relazione inversa






