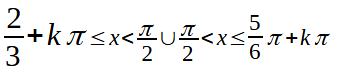DISEQUAZIONI OMOLOGHE DI SECONDO GRADO IN SENO E COSENO
In questa lezione vediamo come si risolvono le DISEQUAZIONI OMOLOGHE DI SECONDO GRADO IN SENO E COSENO e lo facciamo con un esempio.
Supponiamo di voler risolvere la seguente disequazione:
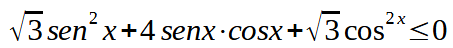
Per risolvere la disequazione dividiamo tutto per cos2 x in modo da ottenre:
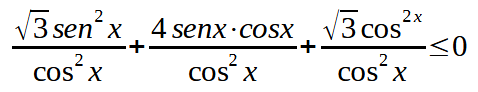
Per poter effettuare tale divisione dobbiamo porre come condizione che
cos2 x ≠0
da cui otteniamo
x ≠ + π/2 + 2kπ
e
x ≠ - π/2 + 2kπ
Dobbiamo prestare attenzione al fatto che tali valori non possono essere soluzioni della nuova disequazione scritta, ma potrebbero essere soluzioni della disequazione di partenza. Per appurarlo andiamo a verificarlo per mezzo di una sostituzione.
Quando
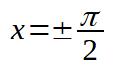
la nostra disequazione diventa:
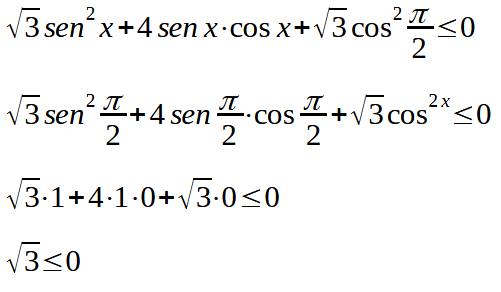
che chiaramente non è mai vera. Quindi tali valori non sono compresi neppure nelle soluzioni della disequazione di partenza.
E ricordando che tan x = sen x/ cos x possiamo scrivere:
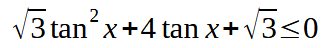
Risolviamo come una normale disequazione di secondo grado.
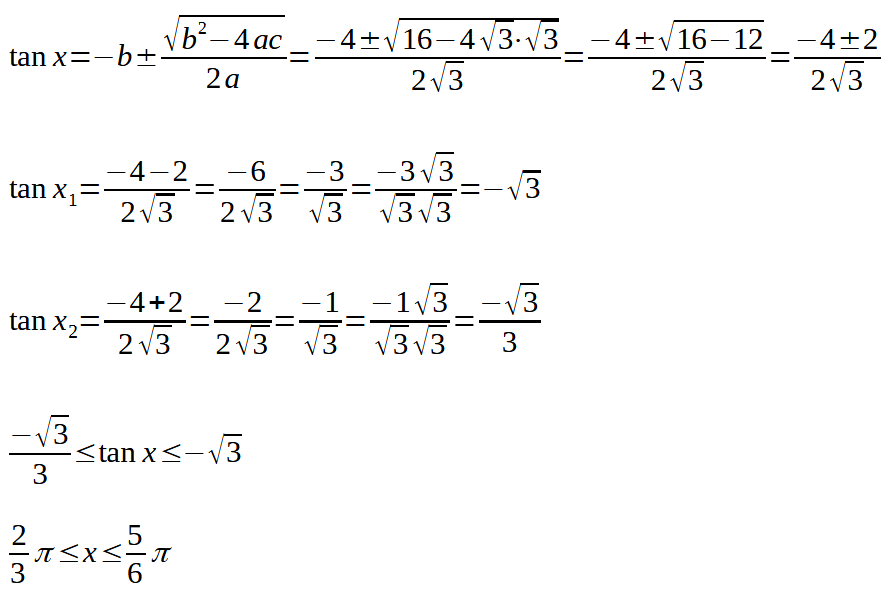
Tenuto conto della periodicità della funzione tangente possiamo scrivere:
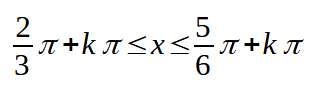
Dobbiamo, però, tenere presente che π/2 deve essere escluso dalle possibili soluzioni.
Quindi la soluzione della disequazione data è