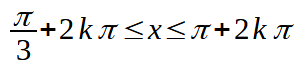DISEQUAZIONI LINEARI IN SENO E COSENO
Le DISEQUAZIONI LINEARI IN SENO E COSENO sono disequazioni di I GRADO nelle quali sono presenti sia la funzione seno che la funzione coseno.
Vediamo come si risolvono disequazioni di questo tipo attraverso un esempio.
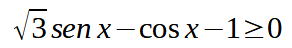
Per risolvere la nostra disequazione utilizziamo le FORMULE PARAMETRICHE del SENO e del COSENO.
Quindi, poniamo:
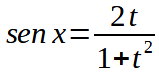
e
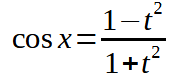
con
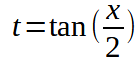
Effettuando le sostituzioni avremo:
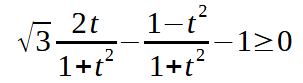
A questo punto dobbiamo porre le condizioni di esistenza della nostra disequazione. Noi sappiamo che la tangente non è definita quando l'angolo è pari a π/2 + kπ.
Nel nostro caso l'angolo è pari a x/2, quindi la condizione di esistenza che dobbiamo porre è:
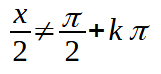
da cui, moltiplicando primo e secondo membro per 2, otteniamo:
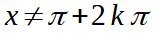
Sicuramente π + 2kπ non può essere una soluzione della nuova disequazione da noi scritta: tuttavia potrebbe essere una soluzione della disequazione di partenza, dato che essa non è una disequazione nella tangente. Per saperlo non dobbiamo fare altro che sostituire tale valore nella disequazione originaria e vedere se essa è verificata. Facciamolo:
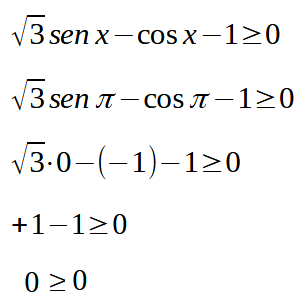
Quindi π è una soluzione ammissibile della nostra disequazione di partenza e di ciò dovremo tenere conto nelle soluzioni finali.
Risolviamo la nuova disequazione da noi scritta:
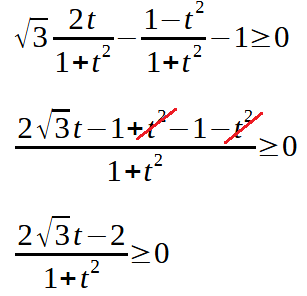
Al denominatore della frazione abbiamo 1 + t2 e, poiché un quadrato (t2) è sempre positivo, se ad esso aggiungiamo 1 avremo sempre un numero positivo. Quindi il denominatore è sempre posititvo.
Di conseguenza, per sapere qual è il segno di tutta la frazione è sufficiente studiare il segno del numeratore e porre:
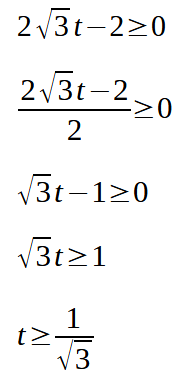
Ma noi sappiamo che:
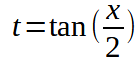
Quindi possiamo scrivere:
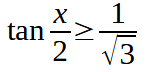
da cui, razionalizzando la frazione avremo:
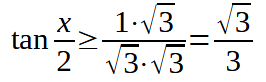
La soluzione della disequazione è:

Teniamo conto della periodicità che nella tangente è π e scriviamo:
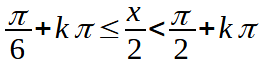
Moltiplichiamo tutti e tre i membri per 2 ed otteniamo:
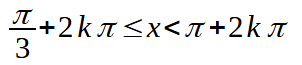
Abbiamo detto, però, che π è una soluzione ammissibile della prima disequazione, quindi dobbiamo includere tale valore nelle soluzioni ammissibili e la nostra soluzione diventa: