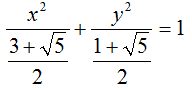SCRIVERE L'EQUAZIONE DELL'ELLISSE PASSANTE PER DUE PUNTI
- L'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle y
- Minimo comune denominatore
- Sistemi di equazioni di secondo grado
Vediamo come possiamo SCRIVERE l'EQUAZIONE di un'ELLISSE quando ci sono date le coordinate del FUOCO dell'ellisse e di un PUNTO per il quale essa passa.
Esempio:
scrivere l'equazione canonica dell'ellisse con fuoco F1 (1; 0) e passante per il punto P(1; 1).
Sappiamo che l'equazione dell'ellisse nella sua forma canonica è

Quindi, per scrivere la nostra equazione, a noi serve sapere il valore di a2 e di b2.
Noi sappiamo che il fuoco ha coordinate del tipo
F (c; 0)
quindi possiamo dire che si tratta di un'ellisse con i FUOCHI situati sull'ASSE DELLE ASCISSE.
Di conseguenza, la relazione che lega a, b, e c sarà:
c2 = a2 - b2.
Sostituendo a c le coordinate del fuoco, avremo:
12 = a2 - b2
1 = a2 - b2.
Sappiamo, inoltre che l'ellisse passa per il punto
P (1; 1).
In questo punto, l'equazione dell'ellisse assume i seguenti valori:
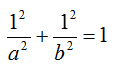
Calcoliamo il minimo comune denominatore a primo membro:
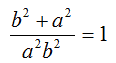
Ora moltiplichiamo primo e secondo membro per a2b2:
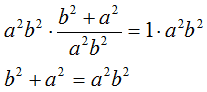
A questo punto risolviamo il sistema formato da quest'ultima equazione e dall'equazione che esprime la relazione tra c, a e b:
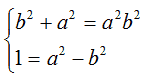
Dalla seconda equazione ricaviamo il valore di b2:
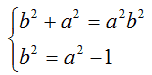
Ora sostituiamo il valore di b2 trovato dalla seconda equazione, nella prima:
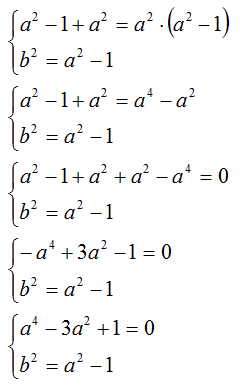
Per risolvere la prima equazione, poniamo:
z = a2.
In questo modo la prima equazione diventa:
z2 - 3z + 1 = 0.
Da cui ricaviamo:
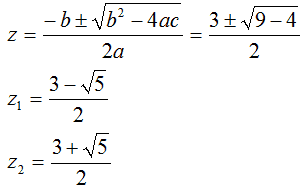
Ora poiché abbiamo posto
z = a2
possiamo scrivere:
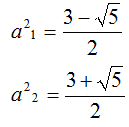
Sostituiamo il valore di a nella seconda equazione del sistema:
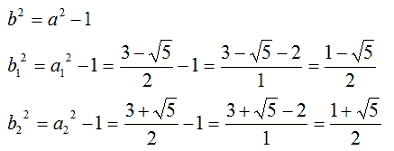
Il primo risultato non è ammissibile perché, come possiamo vedere dallo svolgimento dei calcoli, si tratta di un risultato negativo, e un quadrato non può mai assumere valore negativo:
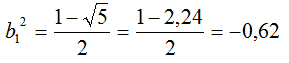
Quindi il risultato da prendere è il secondo b22 e di conseguenza, il valore di a2 da prendere in considerazione sarà a22.
Quindi, l'equazione della nostra ellisse è: