EQUAZIONI IRRAZIONALI CONTENENTI RADICALI QUADRATICI
- Equazioni irrazionali
- Dominio di un'equazione irrazionale
- Come si risolvono le equazioni irrazionali
- Radicali quadratici
- Tipi di equazioni
- Elevamento a potenza
- Equazioni equivalenti
- Soluzioni di un'equazione
- Sistemi di disequazioni di primo grado
Iniziamo a vedere come si risolvono le EQUAZIONI IRRAZIONALI contenenti RADICALI QUADRATICI.
Abbiamo già detto che, per risolvere un'equazione irrazionale occorre elevare entrambi i suoi membri a potenza in modo da eliminare le radici in essa presenti e trasformare l'equazione in un'equazione razionale.
Va detto, però, che quando operiamo la trasformazione di un'EQUAZIONE IRRAZIONALE con RADICALI QUADRATICI in una razionale, NON è detto che otteniamo un'EQUAZIONE EQUIVALENTE a quella data.
Cerchiamo di comprendere meglio questo concetto con degli esempi.
Esempio 1.
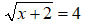
Eleviamo entrambi i membri dell'equazione al quadrato, in modo da eliminare il radicale presente a primo membro. Quindi avremo:
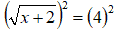
da cui otteniamo
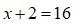
Andiamo a risolvere nei modi consueti:
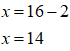
Ora, andiamo a cercare il dominio della nostra equazione di partenza. Esso è dato da
x + 2 ≥ 0
ovvero
x ≥ - 2.
Quindi, la soluzione che abbiamo trovato (cioè x = 14) è una soluzione ammissibile poiché rientra nel campo di esistenza dell'equazione irrazionale: in altre parole è ammissibile perché è superiore (o al più uguale) a 2.
Ora proviamo a sostituire, all'incognita della nostra equazione irrazionale, il risultato trovato. Avremo:
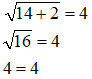
Dunque, in questo primo esempio, la soluzione dell'equazione razionale
x + 2 = 16
è anche soluzione dell'equazione irrazionale data
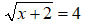
Le due equazioni hanno le stesse soluzioni e, di conseguenza, sono equivalenti.
Esempio 2.
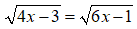
Andiamo ad elevare, entrambi i membri dell'equazione al quadrato
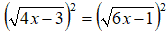
ed otteniamo
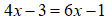
Risolviamo:
4x - 6x = -1 + 3
-2x = +2
2x = -2
x = -2/2
x = -1.
Ora, andiamo a cercare il dominio della equazione irrazionale di partenza. Esso è datoda
4x - 3 ≥ 0
e
6x - 1 ≥ 0.
Mettiamo a sistema e risolviamo:
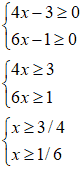

Quindi il dominio della nostra equazione irrazionale è
x ≥ 3/4.
Di conseguenza, la soluzione che abbiamo trovato (cioè x = -1) non è una soluzione ammissibile poiché non rientra nel campo di esistenza dell'equazione: in altre parole non è ammissibile perché è inferiore a 3/4. La nostra equazione, dunque, è impossibile.
Nell'esempio proposto, quindi, l'equazione razionale
4x -3 = 6x - 1
non è equivalente all'equazione irrazionale
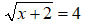
La soluzione della prima equazione (x = -1) è una soluzione ESTRANEA alla seconda. In altre parole, l'equazione irrazionale e quella razionale ottenuta dalla sua trasformazione, non hanno la stessa soluzione.
Esempio 3.

Eleviamo entrambi i membri dell'equazione al quadrato
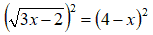
ed otteniamo
3x - 2 = 16 + x2 - 8x
Andiamo a risolvere:
- x2 + 3x + 8x - 2 - 16 = 0
- x2 + 11x - 18 = 0
x2 - 11x + 18 = 0
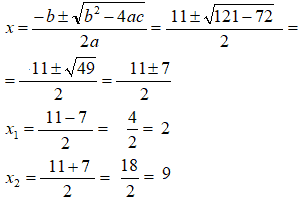
Ora, andiamo a cercare il dominio della equazione irrazionale di partenza. Esso è dato
3x - 2 ≥ 0
3x ≥ 2
x ≥ 2/3.
Entrambe le soluzioni trovate rientrano nel campo di esistenza dell'equazione irrazionale, dato che sia 2 che 9 sono maggiori di 2/3.
Ora, però, andiamo a sostituire i valori trovati all'incognita della equazione irrazionale. Partiamo con il primo risultato:
x = 2
Avremo:
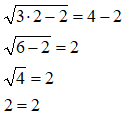
Quindi 2 è una soluzione accettabile.
Passiamo al secondo risultato ottenuto:
x = 9
Avremo:
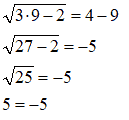
Quindi 9 è una soluzione ESTRANEA all'equazione irrazionale data.
In altre parole, l'equazione razionale ottenuta, elevando al quadrato entrambi i membri dell'equazione irrazionale, non è equivalente a quest'ultima.
Allora chiediamoci: "Come facciamo a sapere se le soluzioni trovate sono anche soluzioni dell'equazione irrazionale di partenza?"
Il modo più semplice è quello di VERIFICARE che le soluzioni ottenute siano anche soluzioni dell'equazione di partenza, andando a sostituire all'incognita dell'equazione irrazionale le soluzioni trovate e SCARTANDO le SOLUZIONI ESTRANEE.
Esiste, però, anche un secondo metodo che consiste nel porre delle condizioni iniziali che ci permettono di avere solamente soluzioni che sono anche soluzioni dell'equazione di partenza. Ma questo lo vedremo nelle lezioni successive.
Infine, potremmo chiederci perché accade che elevando al quadrato entrambi i membri di un'equazione irrazionale non sempre otteniamo un'equazione equivalente a quella data. Risponderemo a questa domanda nella prossima lezione.






