SOTTOMATRICI PRINCIPALI
Data una MATRICE QUADRATA A di ordine n chiamiamo SOTTOMATRICE PRINCIPALE di A una SOTTOMATRICE di A la cui DIAGONALE PRINCIPALE è costituita da ELEMENTI della DIAGONALE PRINCIPALE di A.
Esempio.
Consideriamo la matrice quadrata A

Quella che abbiamo scritto è una matrice quadrata di ordine 4.
La sua DIAGONALE PRINCIPALE è costituita dagli elementi:
3 5 8 3.
Ora cancelliamo dalla matrice A la quarta riga e la quarta colonna in modo da ottenere la sottomatrice A' (che si legge A primo). Avremo:
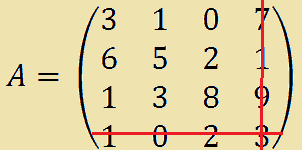
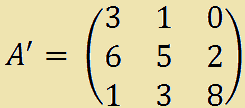
Gli elementi della DIAGONALE PRINCIPALE di A' sono:
3 5 8.
Essi sono anche elementi della diagonale principale di A. Quindi la matrice A' è una SOTTOMATRICE PRINCIPALE di A.
Ma anche
- la matrice B':
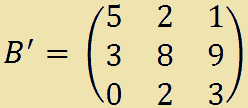
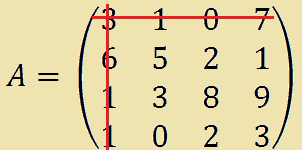
ottenuta dalla matrice A togliendo la prima riga e la prima colonna è una SOTTOMATRICE PRINCIPALE di A.
- come
pure la matrice C':
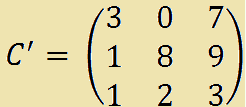
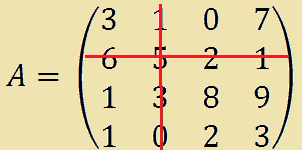
ottenuta dalla matrice A togliendo la seconda riga e la seconda colonna
- e la
matrice D'
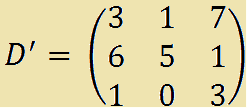
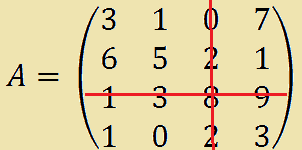
ottenuta dalla matrice A togliendo la terza riga e la terza colonna
sono delle SOTTOMATRICI PRINCIPALI di A.
Nella prossima lezione vedremo che esistono delle sottomatrici principali dette di testa o di guida.






