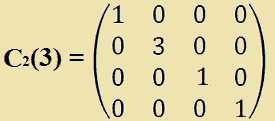OPERAZIONI ELEMENTARI E MATRICI ELEMENTARI
- Matrice
- Rango o caratteristica di una matrice
- Matrici equivalenti
- Matrice elementari
- Matrice identità
Nella lezione precedente abbiamo parlato di MATRICI ELEMENTARI e abbiamo detto che:
- eseguire delle OPERAZIONI ELEMENTARI su una matrice A
- PRE-MOLTIPLICARE o POST-MOLTIPLICARE la MATRICE ELEMENTARE ottenuta da una MATRICE IDENTITA' di ordine opportuno alla quale sono state applicate le operazioni elementari che si vogliono considerare, alla matrice A porta ad ottenere il medesimo risultato.
Ora diciamo che
- occorre PRE-MOLTIPLICARE la matrice elementare per la matrice A se si vuole applicare un OPERAZIONE ELEMENTARE per RIGA;
- occorre POST-MOLTIPLICARE la matrice elementare per la matrice A se si vuole applicare un OPERAZIONE ELEMENTARE per COLONNA.
Esempio.
Sulla matrice A vogliamo eseguire le seguenti operazioni:
-
R12
PRE-MOLTIPLICHIAMO la matrice elementare, ottenuta dalla matrice identità scambiando la prima con la seconda riga, per la matrice A.
-
C2(3)
POST-MOLTIPLICHIAMO la matrice elementare, ottenuta dalla matrice identità moltiplicando la seconda colonna per 3, per la matrice A.
-
R21(5)
PRE-MOLTIPLICHIAMO la matrice elementare, ottenuta dalla matrice identità sommando alla seconda riga la prima moltiplicata per 5, per la matrice A.
Ora ci chiediamo come va scelto l'ORDINE della MATRICE IDENTITA' di partenza.
Poiché dobbiamo eseguire sempre il PRODOTTO tra matrici (la matrice elementare e la matrice data) dobbiamo ricordare che tale operazione è possibile solamente se il numero delle colonne della prima matrice è uguale al numero delle righe della seconda matrice.
Quindi:
- se dobbiamo PRE-MOLTIPLICARE la matrice elementare per la matrice A la matrice elementare, e dunque la matrice identità di partenza, dovrà avere ordine uguale al NUMERO DI RIGHE di A;
- se dobbiamo POST-MOLTIPLICARE la matrice elementare per la matrice A la matrice elementare, e dunque la matrice identità di partenza, dovrà avere ordine uguale al NUMERO DI COLONNE di A.
Ora, posto che la matrice A abbia ordine m x n, e chiamando con E la matrice elementare, avremo:
| OPERAZIONE | ESEMPIO | ORDINE DELLA MATRICE IDENTITA' |
|---|---|---|
| PRE-MOLTIPLICARE | E x Amxn | m |
| POST-MOLTIPLICARE | E x Amxn | n |
Le MATRICI ELEMENTARI vengono indicate con lo STESSO SEGNO usato per indicare la CORRISPONDENTE OPERAZIONE ELEMENTARE.
Ad esempio, nella lezione precedente, la prima matrice elementare ottenuta partendo dalla matrice identità di ordine 3 e scambiando la prima riga con la terza riga viene indicata con il simbolo R13. Ovvero:
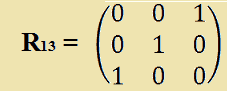
Mentre la seconda matrice elementare ottenuta partendo dalla matrice identità di ordine 4 e moltiplicando la seconda colonna per 3 viene indicata con il simbolo C2(3). Ovvero: