SISTEMI DI EQUAZIONI E MATRICI
- Matrice
- Vettore riga e vettore colonna
- Prodotto tra matrici
- Sistemi di equazioni lineari algebriche
- Sistemi di equazioni equivalenti
- Algoritmo di Kronecker
- Equazioni ridotte a forma normale
Consideriamo il seguente SISTEMA DI EQUAZIONI LINEARI
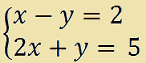
Ora consideriamo la matrice formata dai coefficienti delle due incognite x e y, ricordando che, dove il coefficiente è sottointeso esso è 1 o -1 a seconda del segno che precede l'incognita. Quindi andremo a considerare i seguenti valori:
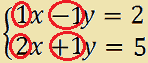
Scriviamo ora la matrice che si ottiene considerando i soli coefficienti delle incognite. Avremo
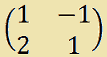
Questa matrice prende il nome di MATRICE DEI COEFFICIENTI.
Ora ORLIAMO la MATRICE DEI COEFFICIENTI con la COLONNA DEI TERMINI NOTI, in altre parole affianchiamo alla matrice dei coefficienti la colonna dei termini noti, cioè:
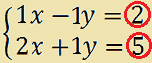
Avremo:

Questa matrice prende il nome di MATRICE COMPLETA.
Mentre il VETTORE COLONNA dei soli TERMINI NOTI sarà:
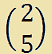
Ora scriviamo il VETTORE COLONNA i cui elementi sono tutte le INCOGNITE che compaiono nel sistema, nel nostro caso x ed y. Esso sarà:
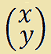
Ora chiamiamo con
A la MATRICE DEI COEFFICIENTI
x il VETTORE DELLE INCOGNITE
b il VETTORE DEI TERMINI NOTI.
Possiamo, allora, scrivere il nostro SISTEMA di partenza nella forma:
A · x = b.
Occorre fare attenzione, quando dobbiamo scrivere la MATRICE DEI COEFFICIENTI o la MATRICE COMPLETA a come è scritto il sistema. Infatti, per prima cosa occorre RIDURRE A FORMA NORMALE tutte le equazioni del sistema se, ovviamente, ve ne è bisogno.
Inoltre occorre indicare, nelle varie equazioni, le INCOGNITE con lo STESSO ORDINE, in modo che siano incolonnate.
Esempio.
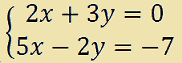
Qui le due equazioni del sistema sono già ridotte a forma normale, quindi possiamo scrivere direttamente la matrice del sistema:
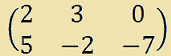
Ora consideriamo il seguente sistema:

Qui bisogna ridurre a forma normale le equazioni e indicare tutte le incognite nello stesso ordine (cioè la x per prima, la y per seconda o viceversa). Ovvero:
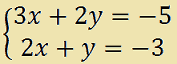
Quindi possiamo scrivere la matrice completa del sistema:







