COTANGENTE
- Circonferenza goniometrica
- Angoli orientati
- Tangente
- Seconda relazione fondamentale della goniometria
Disegniamo la circonferenza goniometrica e l'angolo orientato α:
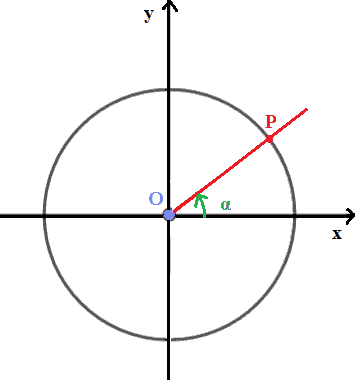
Ora disegniamo la retta TANGENTE alla circonferenza goniometrica nel punto B di coordinate (0 ; 1):

ed indichiamo con H il punto in cui tale retta interseca la retta OP:

Chiamiamo COTANGENTE dell'angolo α l'ASCISSA del punto H e la indichiamo con il simbolo
cotg α
oppure
cot α
o ancora
cotan α
che si leggono tutti
cotangente di alfa

Esiste, però, anche un altro modo di definire la cotangente.
Per farlo osserviamo i triangoli OQP e OBH:

Essi hanno in comune:
- l'angolo che nell'immagine sottostante abbiamo indicato con il colore verde, ovvero l'angolo consecutivo all'angolo α;
- inoltre, entrambi i triangoli hanno un angolo retto:
- quello con vertice nel punto Q, nel caso del triangolo OQP. Essendo la retta PQ perpendicolare all'asse delle ascisse, forma con essa 4 angoli retti;
- quello con vertice nel punto B, nel caso del triangolo OBH. Infatti, una retta tangente alla circonferenza forma con, il raggio della circonferenza, quattro angoli retti, essendo la tangente perpendicolare al raggio.

Ma noi sappiamo che due triangoli che hanno due angoli ordinatamente congruenti sono SIMILI tra loro.

Di conseguenza, questi due triangoli hanno i LATI CORRISPONDENTI PROPORZIONALI. Quindi saranno tra loro proporzionali:
- il lato BH del triangolo OBH con
il lato QP del triangolo OQP

- e il lato OB del triangolo OBH con
il lato OQ del triangolo OQP

Pertanto possiamo scrivere la seguente proporzione:
BH : OB = QP : OQ
Dove:
- i termini a sinistra del simbolo = indicano i due CATETI del triangolo OBH;
- mentre i termini a destra del simbolo = indicano i due CATETI del triangolo OQP.
Ma noi sappiamo che:
- OB è il RAGGIO della circonferenza goniometrica che è uguale a 1;
- QP è il COSENO dell'angolo α;
- OQ è il SENO dell'angolo α;
Quindi la nostra proporzione può essere scritta nel modo seguente:
BH : 1 = cos α : sen α
Ma BH è la COTANGENTE dell'angolo α. Quindi possiamo scrivere:
cot α : 1 = cos α : sen α
da cui otteniamo:
cot α · sen α = 1 · cos α
Dividendo entrambi i membri della nostra proprozione, per sen α, avremo:

Quindi possiamo dire che la CONTANGENTE di un angolo non è altro che il RAPPORTO tra il COSENO e il SENO dell'angolo stesso.
Dallo studio della TANGENTE, e in modo particolare della seconda relazione fondamentale della goniometria sappiamo che:
tan α = sen α/ cos α
E' evidente, allora, che la COTANGENTE non è altro che la FUNZIONE RECIPROCA della TANGENTE. Infatti, essendo

il reciproco del primo e del secondo membro diventano:

che non è altro che la COTANGENTE:







