GLI ANGOLI NOTEVOLI E L'ANGOLO DI 30°
Nelle lezioni precedenti abbiamo visto come variano il seno, il coseno, la tangente e la cotangente al variare dell'angolo α e abbiamo visto il valore che tali funzioni goniometriche assumono per l'angolo di 0°, di 90°, di 180° e di 270°.
E per gli altri angoli, come si determina il valore delle funzioni goniometriche?
Vi sono alcuni particolari angoli, per i quali i valori delle funzioni goniometriche possono essere determinati grazie a delle relazioni geometriche: tali angoli sono detti ANGOLI NOTEVOLI.
Iniziamo con l'angolo di 30°, che sappiamo corrisponde a π/6 RADIANTI.

Costruiamo il triangolo PHO:

L'angolo con vertice in H è un angolo retto essondo il segmento PH perpendicolare all'asse delle ascisse.
Il triangolo è, quindi, un TRIANGOLO RETTANGOLO.
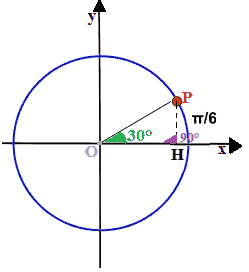
Noi conosciamo la misura dell'angolo con vertice in O, che ha um'ampiezza di 30°, e la misura dell'angolo con vertice in H che, essendo retto misura 90°. Poiché la somma degli angoli interni del triangolo è pari a 180°, possiamo dire con certezza che l'angolo con vertice in P misura 60° (infatti 180° - 30° - 90° = 60°).

Se ribaltiamo il triangolo PHO attorno all'asse delle x otteniamo il triangolo PP'O che è un TRIANGOLO EQUILATERO dato che i suoi angoli misurano tutti e tre 60°.

Noi sappiamo che il lato OP, essendo il raggio della circonferenza goniometrica, è uguale a 1.
Poiché il triangolo è equilatero, tutti e tre i suoi lati, sono pari ad 1: quindi anche il segmento PP'. E siccome il segmento PH è la metà di PP', esso sarà pari a 1/2.
Sappiamo che PH è il SENO dell'angolo di 30°: quindi esso è pari a 1/2.
Occupiamoci ora del coseno.
Il coseno dell'angolo di 30° è dato dal segmento OH.
Poichè abbiamo la misura di OP e OH, applicando il teorema di Pitagora possiamo trovare il valore di OH.
Quindi:

Una volta noto anche il coseno, possiamo determinare la tangente. Essa è uguale a:

Eliminiamo la radice dal denominatore della frazione moltiplicando numeratore e denominatore per la radice quadrata di 3. Si avrà:

Non ci resta che determinare la cotangente: essa è il reciproco della tangente che abbiamo visto non è altro che il rapporto tra 1 e la radice di 3. Quindi:

Chiaramente possiamo determinare anche la secante, che è uguale a:

Moltiplicando numeratore e denominatore per la radice di tre si ottiene:

E per finire andiamo a determinare anche la cosecante:

Nelle prossime lezioni andremo a vedere i valori delle funzioni goniometriche di altri angoli notevoli.






