AREA DI UN POLIGONO REGOLARE
- Area dei poligoni
- Area del triangolo
- Area del triangolo e formule inverse
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Misure di superficie
- Triangoli
- Figure geometriche equivalenti e figure geometriche congruenti
- Apotema di un poligono
- Rette perpendicolari
- Perimetro di un poligono
Disegniamo un POLIGONO REGOLARE, cioè un POLIGONO EQUIANGOLO ed EQUILATERO, ad esempio disegniamo l'ESAGONO ABCDEF:
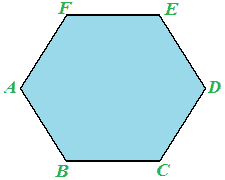
Ora congiungiamo il centro del poligono con ciascun vertice:

Notiamo che l'esagono risulta così suddiviso in 6 TRIANGOLI CONGRUENTI.
La BASE di ogni TRIANGOLO coincide con il LATO dell'esagono (che nell'immagine sottostante abbiamo indicato con l).
L'ALTEZZA di ogni TRIANGOLO non è altro che l'APOTEMA dell'esagono, cioè il segmento che parte dal CENTRO del POLIGONO e cade PERPENDICOLARMENTE su uno dei suoi LATI (nell'immagine sottostante abbiamo indicato l'apotema con a).

L'AREA di uno dei sei TRIANGOLI si trova applicando la formula:
AT = (b x h)/ 2
dove
AT = area di un triangolo
b = base del triangolo
h = altezza del triangolo.
Ma abbiamo detto che
b = l
cioè la base del triangolo coincide con il lato dell'esagono
e
h = a
cioè l'altezza del triangolo coincide con l'apotema dell'esagono.
Quindi, sostituiamo nella formula precedente e abbiamo
AT = (l x a)/ 2.
In questo modo troviamo l'area di un triangolo. Poiché l'esagono è formato da 6 triangoli, la sua area sarà:
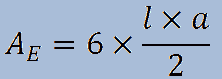
dove
AE = area dell'esagono.
Ma
6 x l
non è altro che il PERIMETRO dell'esagono.
Quindi, se indichiamo con P il perimetro possiamo scrivere:
AE = (P x a)/ 2.
In altre parole l'AREA dell'ESAGONO si ottiene MOLTIPLICANDO il suo PERIMETRO per l'APOTEMA e DIVIDENDO il risultato per 2.
Nel nostro esempio abbiamo parlato dell'esagono, ma la regola appena vista vale anche per gli altri poligoni regolari.
Quindi, generalizzando, l'area di un poligono regolare è data da:
A = (P x a)/ 2.
Esempio:
Calcolare l'area di un pentagono regolare che ha il lato di cm 4 e l'apotema di cm 2,5.
Per calcolare l'area iniziamo col calcolare il perimetro del nostro poligono. Poiché il pentagono ha cinque lati, il perimetro sarà dato da:
P = cm 4 x 5 = cm 20.
Ora applichiamo la formula per trovare l'area:
A = (P x a)/ 2 = (20 x 2,5)/ 2 = cm2 25.
Nella prossima lezione ci occuperemo delle formule inverse.






