DISEQUAZIONI GONIOMETRICHE ELEMENTARI NEL SENO
- Disequazioni goniometriche
- Disequazioni goniometriche elementari
- Circonferenza goniometrica;
- Grafico della funzione seno
Iniziamo a capire come si risolvono le disequazioni goniometriche elementari partendo dalle disequazioni nel SENO che si presentano in uno dei modi seguenti:
sen x < a
sen x > a
sen x ≤ a.
sen x ≥ a
con a ∈ R
che si legge
con a appartenente all'insieme dei numeri reali.
Come abbiamo già avuto modo di dire, la prima cosa da fare quando dobbiamo risolvere una disequazione goniometrica è quella di porre le CONDIZIONI DI ESISTENZA: la funzione seno è sempre definita. Quindi i risultati che otterremo risolvendo la disequazione sono tutti accettabili.
Abbiamo visto, nella lezione precedente, che esistono due metodi diversi per risolvere questo tipo di disequazione. Vediamoli entrambi.
1° METODO - RISOLUZIONE CON IL GRAFICO DELLA FUNZIONE GONIOMETRICA
Con il primo metodo per risolvere la disequazione occorre:
- DISEGNARE IL GRAFICO DELLA FUNZIONE seno;
- DISEGNARE l'EQUAZIONE della RETTA y = a;
- le SOLUZIONI della disequazioni sono date dalle ASCISSE dei PUNTI del grafico che si trovano SOPRA o SOTTO la retta y = a a seconda del verso della diseguaglianza.
Supponiamo di voler risolvere la disequazione:
sen x > 1/2
Iniziamo col disegnare il grafico della funzione seno nell'intervallo [0, 2π[ (l'estremo 0 è compreso nell'intervallo, mentre l'estremo 2π è escluso dato che coincide con l'angolo 0)
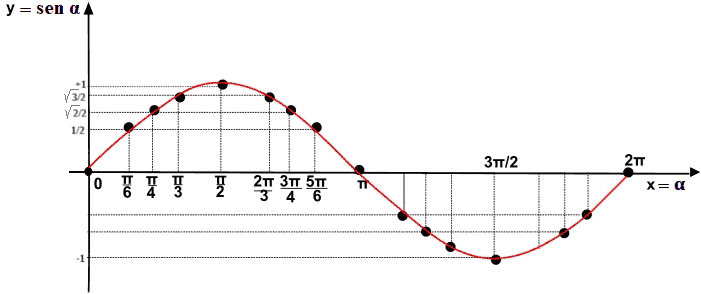
Sullo stesso grafico disegniamo la retta y = 1/2
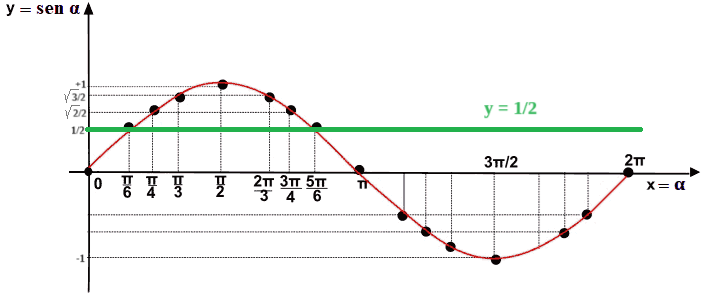
Ora andiamo a cercare le soluzioni chiedendoci quando il seno di x risulta essere maggiore di 1/2. Evidenziamo questa porzione del grafico tracciando la funzione del seno col colore blu.
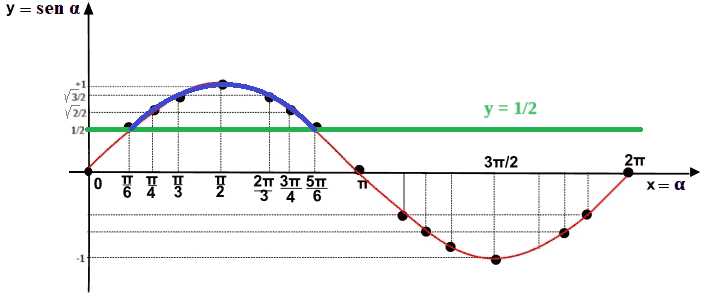
Notiamo che, la funzione seno di x è maggiore di 1/2 quando la x assume valori compresi tra π/6 e 5π/6.
I due estremi del nostro intervallo sono esclusi dalla soluzione, poiché quando il seno è pari a π/6 o a 5π/6 il seno assume valore 1/2, mentre noi stiamo cercando i valori del seno di x superiori ad 1/2.
Poiché l'intervallo dopo il quale la funzione seno si ripete è 2π, la nostra soluzione diventa:
π/6 + 2kπ < x < 5π/6 + 2kπ.
Ovviamente, lo stesso risultato può essere scritto nel modo seguente:
]π/6 + 2kπ ; 5π/6 + 2kπ[.
2° METODO - RISOLUZIONE CON LA CIRCONFERENZA GONIOMETRICA
Con il secondo metodo per risolvere la disequazione occorre:
- DISEGNARE la CIRCONFERENZA GONIOMETRICA;
- INDIVIDUARE, sulla circonferenza goniometrica, i punti aventi come ordinata a;
- DETERMININARE gli ARCHI in cui la disequazione è soddisfatta.
Riprendiamo la disequazione vista prima:
sen x > 1/2
Iniziamo col disegnare la circonferenza goniometrica:
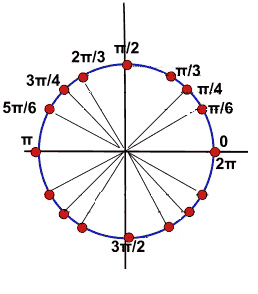
Tracciamo la retta y = 1/2 ed individuiamo i punti A e B che hanno tale ordinata:
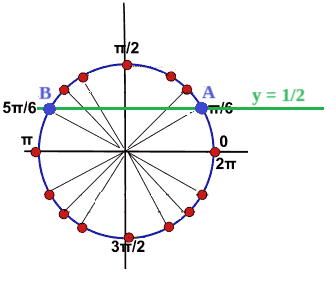
L'angolo individuato dal punto A è l'angolo π/6, mentre l'angolo individuato dal punto B è l'angolo 5π/6.
Ora individuiamo, sulla circonferenza goniometrica, tutti i punti che hanno ordinata maggiore di 1/2 e li evidenziamo di verde:
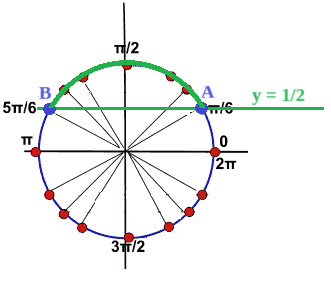
La soluzione della nostra disequazione è data da tutti gli angoli a cui corrispondono sulla circonferenza goniometrica i punti evidenziati in verde. La soluzione, quindi, è:
]π/6 ; 5π/6[.
Anche in questo caso escludiamo gli estremi dell'intervallo, dato che stiamo cercando i valori di x tali che il seno di x è maggiore di 1/2, escludendo il caso in cui esso è uguale ad 1/2.
Tenendo conto della periodocità della funzione seno, avremo:
]π/6 + 2kπ ; 5π/6 + 2kπ[






