DISEQUAZIONI GONIOMETRICHE ELEMENTARI NEL COSENO
- Disequazioni goniometriche
- Disequazioni goniometriche elementari
- Circonferenza goniometrica;
- Grafico della funzione coseno
In questa lezione andremo a vedere come si risolvono le disequazioni goniometriche elementari nel COSENO che si presentano in uno dei modi seguenti:
cos x < b
cos x > b
cos x ≤ b.
cos x ≥ b.
con b ∈ R
che si legge
con b appartenente all'insieme dei numeri reali.
Per prima cosa andiamo a vedere quali sono le CONDIZIONI DI ESISTENZA della disequazione: la funzione coseno è sempre definita. Quindi i risultati che otterremo dalla soluzione della disequazione sono tutti ammissibili.
Vediamo come possiamo risolvere disequazioni di questo tipo sia utilizzando il grafico della funzione goniometrica che usando la circonferenza goniometrica.
1° METODO - RISOLUZIONE CON IL GRAFICO DELLA FUNZIONE GONIOMETRICA
Supponiamo di voler risolvere la disequazione:
cos x > 1
Iniziamo col disegnare il GRAFICO DELLA FUNZIONE COSENO nell'intervallo [0, 2π[ (l'estremo 0 è compreso nell'intervallo, mentre l'estremo 2π è escluso dato che coincide con l'angolo 0)
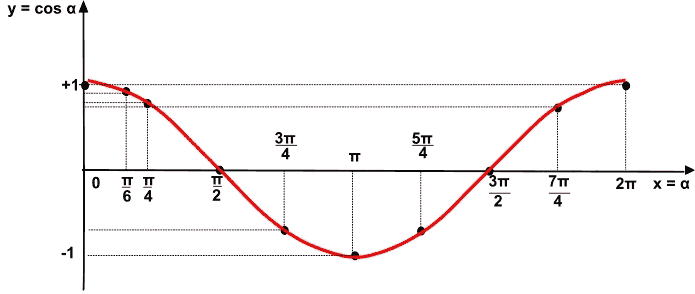
Sullo stesso grafico disegniamo la retta y = 1
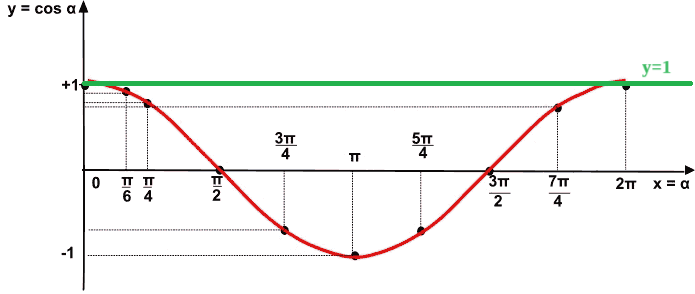
Ora andiamo a cercare le soluzioni chiedendoci quando il coseno di x risulta essere uguale o maggiore di 1.
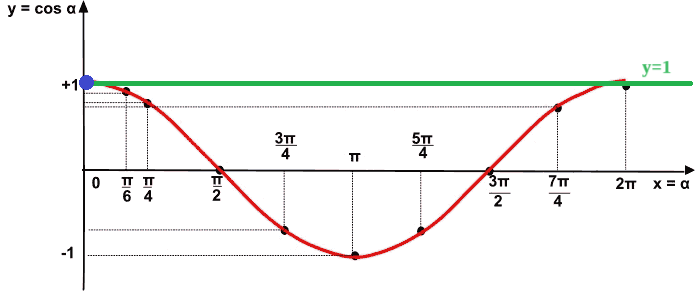
E' evidente che il coseno di x non è mai maggiore di 1, mentre assume il valore 1 quando l'angolo è pari a 0.
Ovvero:
x = 0.
Poiché l'intervallo dopo il quale la funzione coseno si ripete è 2π, la nostra soluzione diventa:
x = 0 + 2kπ
che equivale a scrivere:
x = 2kπ
2° METODO - RISOLUZIONE CON LA CIRCONFERENZA GONIOMETRICA
Vediamo, ora, come possiamo risolvere la stessa disequazione utilizzando la circonferenza goniometrica.
Iniziamo col disegnare la circonferenza goniometrica:
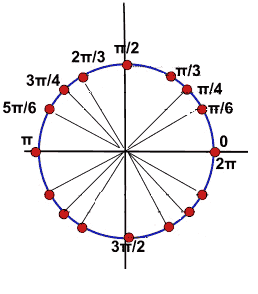
Ora disegniamo la retta x = 1 ed individuiamo i punti che hanno tale ascissa:
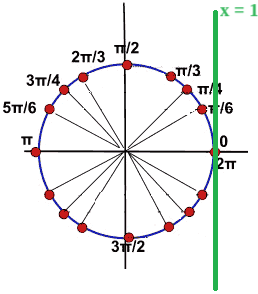
L'unico punto della circonferenza goniometrica che ha come ascissa 1 è il punto A
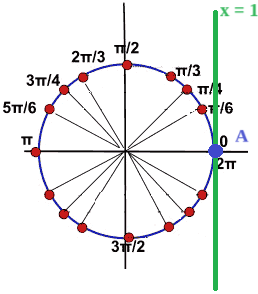
L'angolo individuato dal punto A è l'angolo 0.
Non abbiamo, sulla nostra circonferenza goniometrica, dei punti che hanno un'ascissa maggiore di 1 quindi la soluzione della disequazione è
x = 0.
che, tenendo conto della periodocità della funzione coseno, diventa:
x = 0 + 2kπ
che equivale a scrivere
x = 2kπ






