DISEQUAZIONI GONIOMETRICHE ELEMENTARI NELLA COSECANTE
Concludiamo l'esame delle disequazioni goniometriche elementari parlando delle disequazioni goniometriche elementari nella COSECANTE.
Queste disequazioni si possono presentare in uno dei modi seguenti:
cosec x < f
cosec x > f
cosec x ≤ f
cosec x ≥ f
con f ∈ R
che si legge
con f appartenente all'insieme dei numeri reali.
Iniziamo col vedere le CONDIZIONI DI ESISTENZA: nell'intervallo [0 , π[ la funzione cosecante non è definita quando l'angolo è pari a 0, π, 2π. Quindi questi valori non possono essere soluzioni della disequazione data.
Supponiamo di voler risolvere la disequazione:
cosec x >1
Iniziamo col disegnare il GRAFICO DELLA FUNZIONE COSECANTE nell'intervallo [0, 2π[ (l'estremo 0 è compreso nell'intervallo, mentre l'estremo 2π è escluso dato che coincide con l'angolo 0)
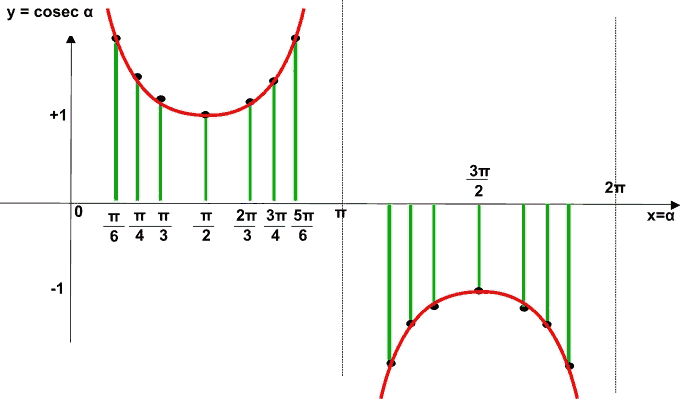
Sullo stesso grafico andiamo a disegnare la retta y = 1:
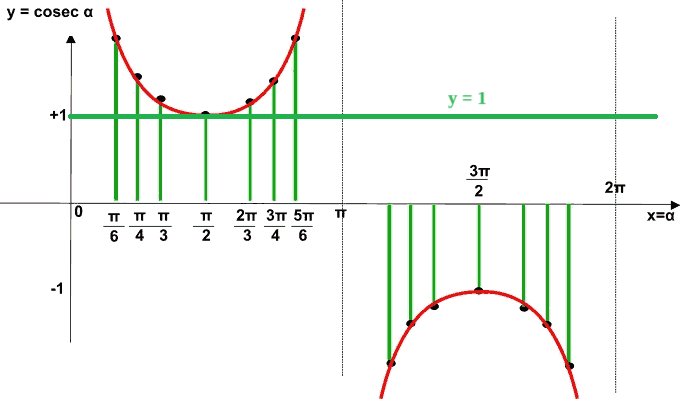
Le soluzioni della nostra disequazione sono rappresentate da tutti i punti situati al di sopra della retta appena disegnata, cioè dai punti che nel grafico sottostante abbiamo indicato con il colore blu.
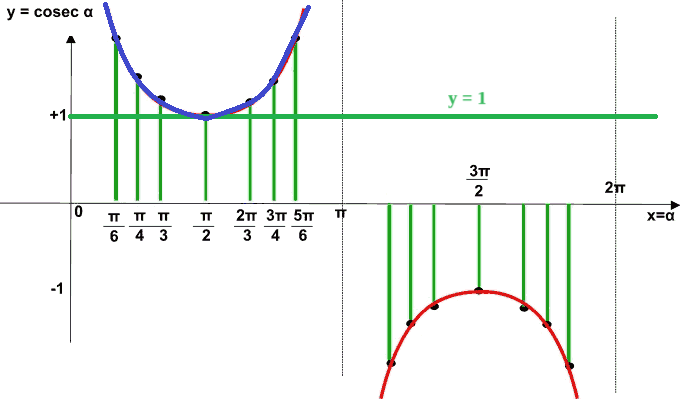
Si tratta di tutti i valori compresi tra 0 e π con i due estremi esclusi, per rispettare le condizioni di esistenza poste inizialmente.
Dato che la funzione cosecante si ripete sempre allo stesso modo dopo un periodo di 2π, la soluzione della nostra disequazione è
2kπ < x < π + 2kπ
Anche in questo caso la soluzione può essere espressa mediante gli intervalli, nel modo seguente:
]2kπ ; π + 2kπ[
Entrambe le parentesi sono aperte, perché nessuno dei due estremi è compreso nell'intervallo delle soluzioni.






