DISEQUAZIONI GONIOMETRICHE ELEMENTARI NELLA SECANTE
Vediamo, in questa lezione, come si risolvono le disequazioni goniometriche elementari nella SECANTE.
Queste disequazioni si possono presentare in uno dei modi seguenti:
sec x < e
sec x > e
sec x ≤ e
sec x ≥ e
con e ∈ R
che si legge
con e appartenente all'insieme dei numeri reali.
Partiamo dalle CONDIZIONI DI ESISTENZA: nell'intervallo [0 , π[ la funzione secante non è definita quando l'angolo è pari a π/2 e a 3π/2. Quindi, questi valori vanno esclusi dalle possibili soluzioni della disequazione.
Una volta posta la condizione di esistenza si procede alla risoluzione della disequazione con il metodo del grafico della funzione, così come abbiamo visto nelle lezioni precedenti.
Supponiamo di voler risolvere la disequazione:
sec x > 0
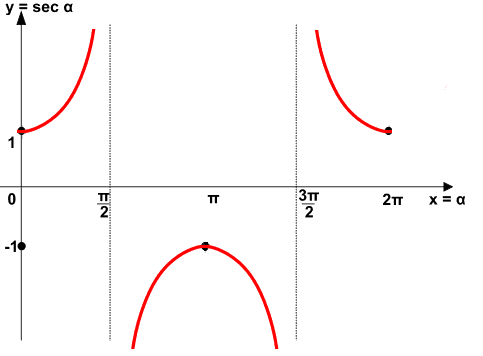
Disegniamo il GRAFICO DELLA FUNZIONE SECANTE nell'intervallo [0, 2π[ (l'estremo 0 è compreso nell'intervallo, mentre l'estremo 2π è escluso dato che coincide con l'angolo 0)
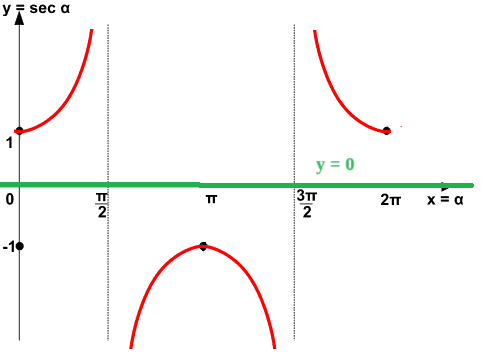
Sullo stesso grafico andiamo a disegnare la retta y = 0 che coincide con l'asse delle x.
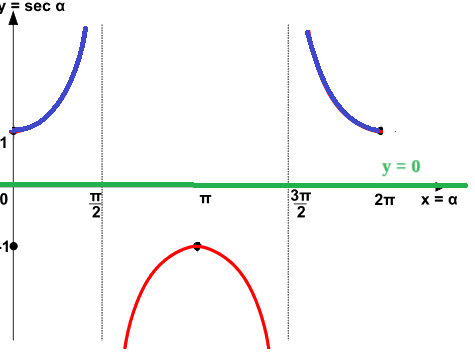
E' evidente che la soluzione della nostra disequazione è data da tutti i valori di x che rendono positiva la secante: si tratta, cioè, di quei valori per i quali la secante è collocata al di sopra dell'asse delle ascisse. Nel grafico sottostante abbiamo disegnato tali punti in blu.
Quindi la nostra soluzione è
0 ≤ x ≤ π/2 ∪ 3π/2 ≤ x ≤ 2π
(Ricordiamo che il simbolo ∪ si legge unito con).
Per le condizioni di esistenza poste dobbiamo escludere dai risultati i valori di π/2 e 3π/2.
Quindi la nostra soluzione diventa:
0 ≤ x < π/2 ∪ 3π/2 < x ≤ 2π
Tenuto conto che la funzione secante si ripete sempre allo stesso modo dopo un periodo di 2π, la soluzione
2kπ ≤ x < π/2 + 2kπ ∪ 3π/2 + 2kπ < x ≤ 2π + 2kπ
Avremmo potuto scrivere la soluzione anche nel modo seguente:
[2kπ ; π/2 + 2kπ[ ∪ ]3π/2 + 2kπ ; 2π + 2kπ]






