TEOREMA DI PITAGORA E TRIANGOLO ISOSCELE RETTANGOLO
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Triangolo rettangolo
- Triangolo isoscele rettangolo
- Figure geometriche equivalenti e figure geometriche congruenti
- Estrazione di radice quadrata: casi particolari
- Estrazione di radice quadrata: casi particolari
Studiando i triangoli isosceli abbiamo appreso che un tipo particolare di triangolo isoscele è il TRIANGOLO ISOSCELE RETTANGOLO, cioè un triangolo che ha:
- DUE LATI CONGRUENTI;
- UN ANGOLO RETTO.

E' evidente, quindi, che nel nostro triangolo i due CATETI sonoCONGRUENTI.
Il TEOREMA DI PITAGORA ci dice che:
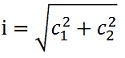
dove
i = ipotenusa
c1 = un cateto
c2 = l'altro cateto.
Ora noi sappiamo che i due cateti sono congruenti, quindi la misura di c1 e c2 è la stessa. Pertanto possiamo scrivere che:
c1 = c2
Ora indichiamo con
c
la misura del cateto e lo sostituiamo nella formula precedente che diventa:
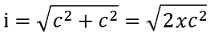
Noi sappiamo che la radice quadrata di un prodotto è uguale al prodotto delle radici quadrate dei singoli fattori. Quindi possiamo scrivere:
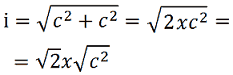
Ma sappiamo anche che la radice quadrata del quadrato di un numero è uguale alla sua base, quindi la radice quadrata di c2 è uguale a c. Quindi, la nostra formula diventa:
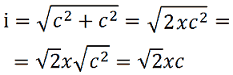
Inoltre, sapendo che la radice quadrata di 2 è pari, all'incirca, a 1,414 possiamo scrivere:
i = 1,414 x c.
Da questa formula possiamo ricavare quella che ci permette di trovare il cateto conoscendo l'ipotenusa.
Essa è:
c = i/ 1,414.






