COME RISOLVERE UN TRIANGOLO RETTANGOLO SE CONOSCIAMO UN CATETO E L'IPOTENUSA
- Relazioni trigonometriche per un triangolo rettangolo
- Secondo teorema dei triangoli rettangoli
- Risoluzione dei triangoli rettangoli
Nella lezione precedente abbiamo visto cosa significa RISOLVERE UN TRIANGOLO RETTANGOLO e come applicare le relazioni trigonometriche per un triangolo rettangolo nel caso in cui sono noti due lati del triangolo.
In questa lezione vedremo come possiamo RISOLVERE UN TRIANGOLO RETTANGOLO se conosciamo la misura di un CATETO e dell'IPOTENUSA.
Esempio:
dato il TRIANGOLO RETTANGOLO ABC, rettangolo in
A, e sapendo che uno dei cateti è lungo 10 cm, mentre l'ipotenusa è lunga 26 cm, risolviamo il triangolo.
Disegniamo il triangolo:
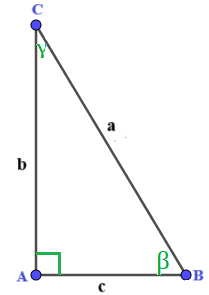
I dati a nostra disposizione sono:
- triancolo ABC, rettangolo in A;
- ipotenusa BC = a = 48 cm;
- cateto AC = b = 24 cm.
Noi dobbiamo trovare l'altro cateto e la misura dei due angoli β e γ.
Quindi, a noi sono NOTI la misura di un CATETO e quella dell'IPOTENUSA.
Applicando il TEOREMA DI PITAGORA possiamo trovare la misura dell'ALTRO CATETO.
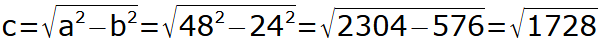
Scomponiamo in fattori primi il numero 1.728 ed eseguiamo i calcoli:
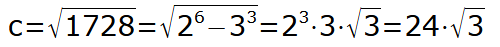
Una volta trovata la misura dell'altro cateto, andiamo a determinare la misura degli angoli β e γ.
Per farlo usiamo il PRIMO TEOREMA DEI TRIANGOLI RETTANGOLI che afferma che IN UN TRIANGOLO RETTANGOLO LA MISURA DI UN CATETO E' UGUALE A QUELLA DELL'IPOTENUSA MOLTIPLICATA PER IL SENO DELL'ANGOLO OPPOSTO AL CATETO. In altre parole noi possiamo scrivere che:
b = a · sen β
da cui possiamo scrivere che:
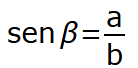
Sostituendo i dati del problema abbiamo:
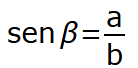
L'angolo β, il cui seno è pari ad 1/2 è l'angolo di 30°.
A questo punto non ci resta che determinare l'ampiezza del terzo angolo. Poiché la SOMMA DEGLI ANGOLI INTERNI DI UN TRIANGOLO È PARI A 180° e dato che conosciamo la misura di due angoli (uno di 90° e l'altro di 30°), possiamo determinare l'ampiezza del terzo angolo nel modo seguente:
180° - 90° - 30° = 60°.
Ricapitolando, i risultati sono:
LATI:
a = 48;
b = 24;
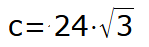
ANGOLI:
α = 90°;
β = 30°;
γ = 60°.
