EQUAZIONI LOGARITMICHE SOTTO FORMA DI UGUAGLIANZA DI DUE LOGARITMI AVENTI LA STESSA BASE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

Iniziamo a vedere come si risolvono le EQUAZIONI LOGARITMICHE partendo da quelle che possono essere ricondotte, mediante la definizione stessa di logaritmo o mediante le proprietà e i teoremi dei logaritmi, alla forma

log_a f(x) = log_a g(x)

L'equazione si presenta come l'uguaglianza di due logaritmi aventi la stessa base. Evidentemente essi possono essere uguali solamente se sono UGUALI gli ARGOMENTI. Quindi, per risolvere l'equazione sarà sufficiente risolvere

f(x) = g(x).

Occorre però fare attenzione perché non tutte le soluzioni ottenute sono necessariamente anche soluzioni della equazione logaritmica. Infatti, noi sappiamo che dato

log_a b

è necessario che

a > 0

a ≠ 1

b > 0.

Ora, tralasciamo la base a che, essendo nota, sicuramente sarà positiva e diversa da 1, e concentriamoci sull'argomento.

Poiché noi andiamo a risolvere

f(x) = g(x)

e non l'equazione di partenza

log_a f(x) = log_a g(x)

potrebbe accadere di trovare dei valori di x tali che rendono l'argomento nullo o minore di zero. Tali valori devono essere esclusi in quanto non possono essere soluzioni dell'equazione di partenza.

Per escludere questi valori possiamo procedere in due modi diversi:

possiamo risolvere l'equazione
f(x) = g(x).

Successivamente andare a SOSTITUIRE i VALORI TROVATI nell'equazione di partenza

log_a f(x) = log_a g(x)

in modo da verificare che i logaritmi ottenuti siano validi. Se, in seguito alla sostituzione, anche uno solo degli argomenti non è positivo, la soluzione non è accettabile;
determinare il CAMPO DI ESISTENZA dell'equazione risolvendo un SISTEMAformato da tante DISEQUAZIONI quanti sono i logaritmi presenti nell'equazione. Ogni equazione dovrà porre la condizione che l'ARGOMENTO di ciascun logaritmo sia POSITIVO.
Una volta ottenute le soluzioni dell'equazione, se esse non appartengono al campo di esistenza devono essere scartate.

Esempio:

log₂(8x+4) = log₂(x-1) + log₂(-x+2).

La prima cosa da fare è cercare, applicando tutte le proprietà e i teoremi da noi conosciuti, di trasformare l'equazione in modo da scriverla nella forma

log_a f(x) = log_a g(x).

A secondo membro, applichiamo il TEOREMA del PRODOTTO DI LOGARITMI:

log₂(8x+4) = log₂[(x-1)(-x+2)].

Eseguiamo i calcoli indicati a secondo membro:

log₂(8x+4) = log₂[(x-1)(-x+2)]

log₂(8x+4) = log₂(-x²+2x + x -2)

log₂(8x+4) = log₂(-x²+3x -2).

Abbiamo ricondotto la nostra equazione alla forma:

log_a f(x) = log_a g(x).

A questo punto possiamo seguire il primo o il secondo metodo indifferentemente: noi li esamineremo entrambi.

Partiamo dal primo metodo di risoluzione: eguagliamo i due argomenti e, una volta trovata la soluzione, la sostituiamo nell'equazione di partenza al fine di verificare che i logaritmi siano validi.

Uguagliamo gli argomenti:

8x+4 = -x²+3x -2.

LA LEZIONE PROSEGUE SOTTO LA PUBBLICITA'

Pubblicità/Advertising

Portiamo tutto a primo membro cambiando di segno:

8x + 4 + x²- 3x + 2 = 0.

Sommiamo i termini simili:

x²+5x + 6 = 0

e risolviamo

Risoluzione equazioni logaritmiche

Abbiamo ottenuto due risultati. Ora dobbiamo sostituirli nell'equazione di partenza per capire se, così facendo, tutti gli argomenti sono positivi.

Partiamo dalla prima soluzione trovata

x₁ = -3

log₂(8x+4) = log₂(x-1) + log₂(-x+2)

log₂[8 (-3)+4] = log₂(-3-1) + log₂(+3+2)

log₂(-24+4) = log₂(--4) + log₂(+5)

log₂(-20) = log₂(-4) + log₂(5).

Come possiamo notare alcuni argomenti sono negativi

log₂(-20) = log₂(-4) + log₂(5).

quindi la soluzione non è accettabile.

Passiamo alla seconda soluzione trovata

x₂ = -2

log₂(8x+4) = log₂(x-1) + log₂(-x+2)

log₂[8 (-2)+4] = log₂(-2-1) + log₂(+2+2)

log₂(-16+4) = log₂(-3) + log₂(+4)

log₂(-12) = log₂(-3) + log₂(4).

Anche in questo caso alcuni argomenti sono negativi

log₂(-12) = log₂(-3) + log₂(5)

quindi, neanche questa soluzione è accettabile.

Di conseguenza la nostra equazione non ammette soluzioni.

Vediamo come avremmo dovuto procedere impiegando il secondo metodo cioè risolvendo un sistema nel quale poniamo come condizione che tutti gli argomenti dei logaritmi siano positivi:

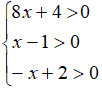
Risoluzione equazioni logaritmiche