EQUAZIONI SIMMETRICHE RISPETTO AL SENO E AL COSENO
- Equazioni goniometriche
- Formula di addizione del seno
- Formula di addizione del coseno
- Prima relazione fodamentale della goniometria
Continuiamo l'esame delle equazioni goniometriche occupandoci, in questa lezione, delle EQUAZIONI GONIOMETRICHE SIMMETRICHE RISPETTO A SENO E COSENO.
Con questo nome intendiamo quelle equazioni goniometriche che NON CAMBIANO CAMBIANDO tra loro il il seno di x con il coseno di x.
Esempio:

Osserviamo cosa accade se, al posto del seno scriviamo il coseno, e viceversa:

E' chiaro che così facendo abbiamo cambiato solo l'ordine dei vari termini, ma l'equazione rimane la stessa.
Queste equazioni si risolvono:
- innanzitutto PONENDO
x = y + π/4
e andando a sostiture, nell'equazione di partenza, alla x il suo nuovo valore.
La scelta di π/4 non è casuale infatti, quando l'angolo è pari a π/4 il seno e il coseno sono uguali;
- successivamente faremo ricorso alle FORMULE DI ADDIZIONE DEL SENO e del COSENO;
- infine, andremo a SEMPLIFICARE l'equazione ottenuta e ad applicare, a seconda dei casi, le FORMULE GONIOMETRICHE o le RELAZIONI FONDAMENTALI DELLA GONIOMETRIA in modo da ottenere un'equazione di quelle esaminate nelle lezioni precedenti.
Torniamo al nostro esempio e vediamo come possiamo procedere.
Per prima cosa poniamo
x = y + π/4.
Effettuando la sostituzione la nostra equazione diventa

A questo punto applichiamo le formule di addizione del seno e del coseno che andiamo a sostituire al posto di
sen (y + π/4) e cos (y + π/4).
Quindi avremo:

Adesso, dove troviamo il seno di π/4 e il coseno di π/4, sostituiamo il valore dall'arco che è pari a radice di due fratto due:
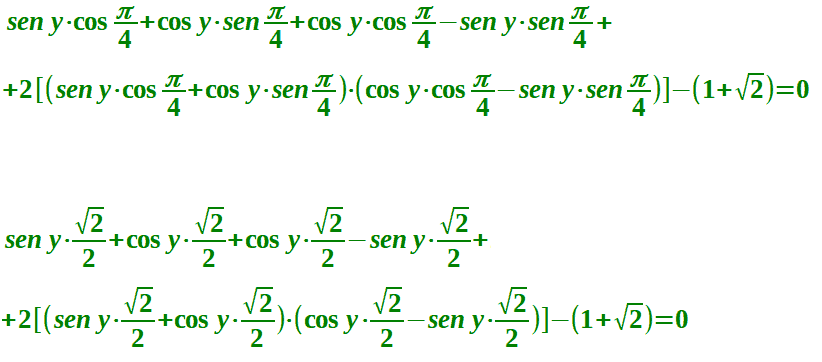
Da qui in poi il modo di procedere può essere diverso a seconda del tipo di equazione: in ogni caso si tratta sempre di semplificare e, come si è detto prima, applicare le formule goniometriche o le relazioni fondamentali della goniometria in modo da essere in grado di risolvere l'equazione.
Noi riscriviamo l'equazione in modo più ordinato ed eseguiamo i calcoli indicati nelle parentesi:

Ora semplifichiamo e sommiamo i termini simili:

Dalla PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA sappiamo che:
1 - cos2 y = sen2 y
che andiamo a sostituire nella nostra equazione:

Semplifichiamo di nuovo in modo da ottenere una equazione goniometrica elementare nel coseno:

Risolviamo e troviamo:
y = 2kπ
Poiché inizialmente avevamo posto:
x = y + π/4
sostituendo abbiamo:
x = π/4 + 2kπ






