EQUAZIONI GONIOMETRICHE ELEMENTARI NELLA COTANGENTE
Dopo aver esaminato, nelle lezioni precedenti, le tre EQUAZIONI GONIOMETRICHE ELEMENTARI:
ora vedremo altre equanzioni goniometriche che, seppure si presentano in forma diversa, si risolvono scrivendole in una delle forme viste sopra.
Partiamo con le EQUAZIONI GONIOMETRICHE ELEMENTARI NELLA COTANGENTE, ovvero con le equazioni che si presentano nella seguente forma:
cot x = n
con
n ∈ R
che si legge
n appartenente all'insieme dei numeri reali.
La prima osservazione che andiamo a fare è che la COTANGENTE AMMETTE SEMPRE SOLUZIONI per qualsiasi numero reale n.
La seconda osservazione che facciamo è che, poiché la cotangente di un angolo non è altro che il rapporto tra il coseno ed il seno dell'angolo stesso, scrivere:
cot x = n
equivale a scrivere
cos x/sen x = n
Quindi, affinché la frazione non perda di significato è necessario che il seno di x sia DIVERSO DA ZERO.
Noi sappiamo che il seno di un arco è diverso da zero, quando l'arco è diverso da kπ, quindi la soluzione da noi trovata dovrà essere
x ≠ kπ
con
Passiamo ora a risolvere la nostra equazione. Per farlo ricordiamo che la cotangente dell'angolo x può essere scritta come 1/tan x. Quindi, risolvere
cot x = n
equivale a risolvere
1/tan x = n.
Ciò significa che la nostra equazione è riconducibile ad un'EQUAZIONE GONIOMETRICA ELEMENTARE NELLA TANGENTE
Infatti:

Quindi risolvere l'equazione:
cot x = n
Equivale a risolvere l'equazione:
tan x = 1/n.
Esempio:

Essa si risolve scrivendo:

Andiamo a RAZIONALIZZARE IL DENOMINATORE DELLA FRAZIONE moltiplicando numeratore e denominatore per la radice di 3:

Quindi si tratta di risolvere l'equazione:
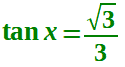
La cui soluzione è:
x = π/6 + kπ
con
Poiché la soluzione trovata è diversa da kπ essa è accettabile.






