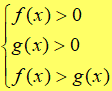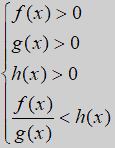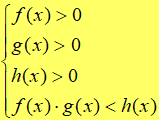EQUAZIONI E DISEQUAZIONI LOGARTMICHE
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Equazioni logaritmiche
- Equazioni logaritmiche sotto forma di uguaglianza di due logaritmi aventi la stessa base
- Equazioni logaritmiche sotto forma di uguaglianza di un logaritmo ed una costante
- Equazioni logaritmiche risolvibili mediante sostituzione
- Equazioni logaritmiche risolvibili con il metodo grafico
- Equazioni logaritmiche risolvibili con logaritmi aventi basi diverse
- Equazioni logaritmiche con l'incognita nella base
- Disequazioni logaritmiche
- Risoluzione di disequazioni logaritmiche
- Disequazioni logaritmiche
- Disequazioni logaritmiche risolvibili mediante i teoremi sui logaritmi
- Disequazioni logaritmiche con un logaritmo ad un membro e lo zero all'altro membro
- Disequazioni logaritmiche con un logaritmo ad un membro ed una costante all'altro membro
- Disequazioni logaritmiche risolvibili mediante sostituzione
- Disequazioni logaritmiche risolvibili con il metodo grafico
Nella tabella che segue sintetizziamo le FORMULE da applicare nella risoluzione delle EQUAZIONI e delle DISEQUAZIONI LOGARITMICHE, rimandando alle lezioni precedenti per un maggiore approfondimento.
EQUAZIONI LOGARITMICHE |
||
|---|---|---|
| EQUAZIONE | SOLUZIONE | LEZIONE |
| loga
f(x) = loga g(x) |
 |
Equazioni logaritmiche sotto forma di uguaglianza di due logaritmi aventi la stessa base |
| loga
f(x) = k |
 |
Equazioni logaritmiche sotto forma di uguaglianza di un logaritmo ed una costante |
| m
· [loga
f(x)]2 + n · loga
f(x) + k = 0 |
 |
Equazioni logaritmiche risolvibili mediante sostituzione |
| loga
f(x) = g(x) |
METODO GRAFICO |
Equazioni logaritmiche risolvibili con il metodo grafico |
| logf(x)
k = h |
 |
Equazioni logaritmiche con l'incognita nella base |
DISEQUAZIONI LOGARITMICHE |
||
|---|---|---|
| DISEQUAZIONE | SOLUZIONE | LEZIONE |
| loga f(x) > loga g(x) | se a > 1
|
Risoluzione di disequazioni logaritmiche |
| se
0 < a < 1
|
||
| loga f(x) < loga g(x) | se
a > 1
|
|
| se
0 < a < 1
|
||
| loga f(x) - loga g(x) > loga h(x) | se
a > 1
|
Disequazioni logaritmiche risolvibili mediante i teoremi sui logaritmi |
| se
0 < a < 1
|
||
| loga f(x) - loga g(x) < loga h(x) | se
a > 1
|
|
| se
0 < a < 1
|
||
| loga f(x) + loga g(x) > loga h(x) | se a > 1
|
Disequazioni logaritmiche risolvibili mediante i teoremi sui logaritmi |
| se
0 < a < 1
|
||
| loga f(x) + loga g(x) < loga h(x) | sea > 1
|
|
| se
0 < a < 1
| ||
| loga f(x) > 0 | se
a > 1
|
Disequazioni logaritmiche con un logaritmo ad un membro e lo zero all'altro membro |
| se
0 < a < 1
|
||
| loga f(x) < 0 | se
a > 1
|
|
| se
0 < a < 1
|
||
| loga f(x) > k | se
a > 1
|
Disequazioni logaritmiche con un logaritmo ad un membro ed una costante all'altro membro |
| se
0 < a < 1
|
||
| loga f(x) < k | se
a > 1
|
|
| se
0 < a < 1
|
||
| m
· [loga
f(x)]2 + n · loga
f(x) + k > 0 |
 |
Disequazioni logaritmiche risolvibili mediante sostituzione |
| m
· [loga
f(x)]2 + n · loga
f(x) + k < 0 | ||
| loga
f(x) > g(x) |
METODO GRAFICO | Disequazioni logaritmiche risolvibili con il metodo grafico |
| loga
f(x) < g(x) |
||